Maße der zentralen Tendenz, Streumaße und Fünf-Punkte Zusammenfassung
Contents
Maße der zentralen Tendenz, Streumaße und Fünf-Punkte Zusammenfassung¶
Berechnen Sie Mittelwert, Standardabweichung, Modalwert des Vektors
data.
data = [10, 1, 17, 0, 14, 2, 11, 1, 4, 10, 5, 1, 1, 99, 47, 16, 3, 4, 9, 11]
Berechnen Sie die Fünf-Punkte-Zusammenfassung für
data.Generieren Sie mit der Funktion
np.linspace()eine \(x\)-Achse mit Werten zwischen \(0\) und \(1\) und stellen Siedataals Streudiagramm dar.Stellen Sie die Daten als Boxplot dar.
Bewerten Sie anhand der Ergebnisse mögliche Ausreißer.
# Frage 1 ...
# Frage 2 ...
# Frage 3 ...
# Frage 4 ...
# Frage 5 ...
Lösungen¶
import numpy as np
import statistics as st
data = [10, 1, 17, 0, 14, 2, 11, 1, 4, 10, 5, 1, 1, 99, 47, 16, 3, 4, 9, 11]
print(f"Mittelwert: {np.mean(data)}")
print(f"Standardabweichung: {np.std(data)}")
print(f"Modalwert: {st.mode(data)}")
Mittelwert: 13.3
Standardabweichung: 22.147460351019934
Modalwert: 1
# Berechne Fünf-Punkte-Zusammenfassung
# Berechne die Quartilen
q1, median, q3 = np.percentile(data, [25, 50, 75])
# Berechne minimal/maximal Datenpunkte
data_min, data_max = min(data), max(data)
# Ausgabe der Daten
print(f"Min: {data_min}")
print(f"Q1: {q1}")
print(f"Median: {median}")
print(f"Q3: {q3}")
print(f"Max: {data_max}")
Min: 0
Q1: 1.75
Median: 7.0
Q3: 11.75
Max: 99
import matplotlib.pyplot as plt
x = np.linspace(0, 1, len(data))
fig, ax = plt.subplots()
ax.scatter(x, data, marker="o")
plt.show()
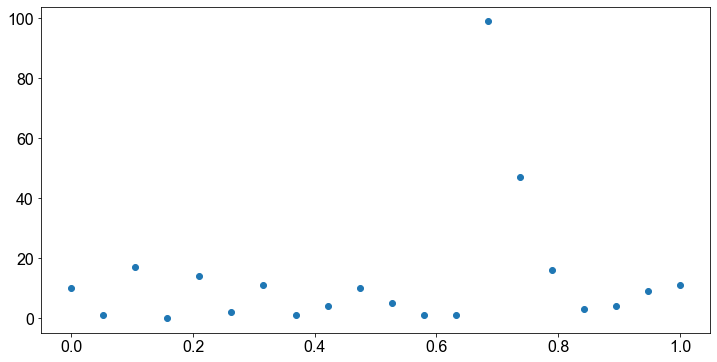
fig, ax = plt.subplots()
ax.boxplot(data)
plt.show()
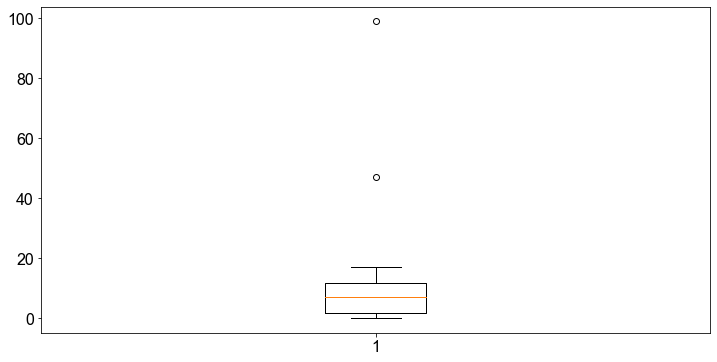
Anhand der visuellen Auswertung von Boxplot und Streudiagram liegt es nahe, dass die Datenpunkte 99 und 27 Ausreißer sind.
