.ipynb .pdf

repository open issue

Binder Live Code

Contents

Hypothesentests

---

Ein sehr häufiges Problem, mit dem Wissenschaftler konfrontiert sind, ist die Bewertung der Signifikanz von verstreuten statistischen Daten. Aufgrund der begrenzten Verfügbarkeit von Beobachtungsdaten wenden Wissenschaftler inferenzstatistische Methoden an, um zu entscheiden, ob die beobachteten Daten signifikante Informationen enthalten oder ob die verstreuten Daten nichts weiter als die Manifestation der inhärent probabilistischen Natur des Datenerzeugungsprozesses sind.

Im Allgemeinen formuliert ein Wissenschaftler ein solches Problem wie folgt. Der Wissenschaftler erstellt ein Modell, das lediglich eine Vereinfachung des Datenerzeugungsprozesses darstellt, und betrachtet eine bestimmte Annahme - eine so genannte Hypothese - dieses Modells. Anhand von Daten will er diese vorläufige Hypothese bewerten.

Bei der Hypothesenprüfung geht es darum, auf der Grundlage von Stichproben aus der Grundgesamtheit statistische Rückschlüsse auf diese Grundgesamtheit zu ziehen. Eine Möglichkeit zur Schätzung eines Grundgesamtheitsparameters ist die Erstellung von Konfidenzintervallen. Eine andere Möglichkeit besteht darin, eine Entscheidung über einen Parameter in Form eines Tests zu treffen. Jeder Hypothesentest erfordert die Erhebung von Daten (Stichproben). Wenn die Hypothese als richtig angenommen wird, kann der Wissenschaftler die erwarteten Ergebnisse eines Experiments berechnen. Weichen die beobachteten Daten erheblich von den erwarteten Ergebnissen ab, so gilt die Annahme als falsch. Auf der Grundlage der beobachteten Daten trifft der Wissenschaftler also eine Entscheidung darüber, ob es aufgrund der Analyse der Daten genügend Beweise dafür gibt, dass das Modell - die Hypothese - verworfen werden sollte, oder ob es keine ausreichenden Beweise für die Verwerfung der angegebenen Hypothese gibt.

Einführung in Hypothesentests

---

In der Inferenzstatistik geht es darum, Entscheidungen oder Urteile über den Wert einer bestimmten Beobachtung oder Messung zu treffen. Eine der am häufigsten verwendeten Methoden, um solche Entscheidungen zu treffen, ist die Durchführung eines Hypothesentests. Eine Hypothese ist ein Erklärungsvorschlag für ein Phänomen. Im Zusammenhang mit statistischen Hypothesentests ist der Begriff Hypothese eine Aussage über etwas, von dem angenommen wird, dass es wahr ist.

Zu einem Hypothesentest gehören zwei Hypothesen: die Nullhypothese und die Alternativhypothese. Die Nullhypothese (\(H_0\)) ist eine zu prüfende Aussage. Die Alternativhypothese (\(H_A\)) ist eine Aussage, die als Alternative zur Nullhypothese betrachtet wird.

Mit dem Hypothesentest soll geprüft werden, ob die Nullhypothese zugunsten der Alternativhypothese verworfen werden sollte. Die grundlegende Logik eines Hypothesentests besteht darin, zwei statistische Datensätze zu vergleichen. Ein Datensatz wird durch eine Stichprobe gewonnen, der andere Datensatz stammt aus einem idealisierten Modell. Wenn die Stichprobendaten mit dem idealisierten Modell übereinstimmen, wird die Nullhypothese nicht verworfen; wenn die Stichprobendaten nicht mit dem idealisierten Modell übereinstimmen und somit eine Alternativhypothese unterstützen, wird die Nullhypothese zugunsten der Alternativhypothese verworfen.

Das Kriterium für die Entscheidung über die Ablehnung der Nullhypothese ist eine so genannte Teststatistik. Die Teststatistik ist eine Zahl, die aus dem Datensatz berechnet wird, der durch Messungen und Beobachtungen oder, allgemeiner, durch Stichproben gewonnen wird.

Formulierung der Hypothese

---

Jeder Hypothesentest beginnt mit der Formulierung der Nullhypothese und der Alternativhypothese. Dieser Abschnitt konzentriert sich auf Hypothesentests für einen Grundgesamtheitsmittelwert, \(\mu\) jedoch gilt das allgemeine Verfahren für jeden Hypothesentest.

Die Nullhypothese für einen Hypothesentest für einen Mittelwert der Grundgesamtheit, \(\mu\) wird ausgedrückt als

\[ H_0: \mu = \mu_0, \]

wobei \(\mu_0\) eine Zahl ist.

Die Formulierung der Alternativhypothese hängt vom Zweck des Hypothesentests ab. Es gibt drei Möglichkeiten, eine Alternativhypothese zu formulieren (Fahrmeir et al. [2016] s.369, Bruce and Bruce [2021] s.97).

Wenn es bei dem Hypothesentest darum geht, zu entscheiden, ob ein Grundgesamtheitsmittelwert von dem angegebenen Wert \(\mu_0\) abweicht, wird die Alternativhypothese wie folgt formuliert

\[H_A: \mu \ne \mu_0\text{.}\]

Ein solcher Hypothesentest wird als zweiseitiger Test bezeichnet.

Wenn es bei dem Hypothesentest darum geht, zu entscheiden, ob der Mittelwert der Grundgesamtheit, \(\mu\) kleiner ist als der angegebene Wert \(\mu_0\), wird die Alternativhypothese wie folgt ausgedrückt

\[H_A: \mu < \mu_0\text{.}\]

Ein solcher Hypothesentest wird als linksseitiger Test bezeichnet.

Geht es bei dem Hypothesentest darum, zu entscheiden, ob der Mittelwert der Grundgesamtheit, \(\mu\) größer als ein bestimmter Wert \(\mu_0\) ist, wird die Alternativhypothese wie folgt ausgedrückt

\[H_A: \mu > \mu_0\text{.}\]

Ein solcher Hypothesentest wird als rechtsseitiger Test bezeichnet.

Man beachte, dass ein Hypothesentest als einseitiger Test bezeichnet wird, wenn er entweder “linksseitig” oder “rechtsseitig” ist.

	zweiseitiger Test	linksseitiger Test	rechtsseitiger Test
Beziehung zwischen \(\mu\), \(\mu_0\) Ablehnung	\(\ne\)	\(\lt\)	\(\gt\)

Fehler vom Typ I, Fehler vom Typ II und Signifikanzniveau

---

Jede Entscheidung, die auf der Grundlage eines Hypothesentests getroffen wird, kann falsch sein. Im Rahmen von Hypothesentests gibt es zwei Arten von Fehlern: Fehler vom Typ I und Fehler vom Typ II. Ein Fehler vom Typ I tritt auf, wenn eine wahre Nullhypothese abgelehnt wird (ein “falsches Positiv”), während ein Fehler vom Typ II auftritt, wenn eine falsche Nullhypothese nicht abgelehnt wird (ein “falsches Negativ”). Mit anderen Worten, ein Fehler vom Typ I besteht darin, dass ein Effekt festgestellt wird, der nicht vorhanden ist, während ein Fehler vom Typ II darin besteht, dass ein Effekt nicht festgestellt wird, der vorhanden ist.

	\(H_0\) trifft zu	\(H_0\) trifft nicht zu
\(H_0\) nicht ablehnen	korrekte Entscheidung	Typ II Fehler
\(H_0\) ablehnen	Typ I Fehler	korrekte Entscheidung

Wenn Sie sich nicht sicher sind, ob es sich um einen Fehler des Typs I oder des Typs II handelt, hilft Ihnen vielleicht eine Illustration (hier).

Die Durchführung eines Hypothesentests bedeutet immer, dass die Möglichkeit besteht, eine falsche Entscheidung zu treffen. Die Wahrscheinlichkeit eines Fehlers vom Typ I (eine wahre Nullhypothese wird abgelehnt) wird allgemein als Signifikanzniveau des Hypothesentests bezeichnet und mit \(\alpha\) angegeben. Die Wahrscheinlichkeit eines Fehlers vom Typ II (eine falsche Nullhypothese wird nicht abgelehnt) wird mit \(\beta\) angegeben. Beachten Sie, dass bei einem festen Stichprobenumfang die Wahrscheinlichkeit \(\beta\) umso größer ist, je kleiner das Signifikanzniveau \(\alpha\) ist, eine falsche Nullhypothese nicht zurückzuweisen (Fahrmeir et al. [2016] s.385).

Das Ergebnis eines Hypothesentests ist eine Aussage zu Gunsten der Nullhypothese oder zu Gunsten der Alternativhypothese. Wenn die Nullhypothese abgelehnt wird, liefern die Daten genügend Beweise, um die Alternativhypothese zu stützen. Wenn die Nullhypothese nicht verworfen wird, liefern die Daten keine ausreichenden Beweise für die Alternativhypothese. Wenn der Hypothesentest auf dem Signifikanzniveau \(\alpha\) durchgeführt wird, kann man sagen, dass die Testergebnisse auf dem \(\alpha\)-Niveau statistisch signifikant sind. Wenn die Nullhypothese auf dem Signifikanzniveau \(\alpha\) nicht abgelehnt wird, kann man sagen, dass die Testergebnisse auf dem \(\alpha\)-Niveau statistisch nicht signifikant sind.

Der kritische Wert und der \(p\)-Wert-Ansatz bei der Hypothesenprüfung

---

Um zu entscheiden, ob die Nullhypothese abzulehnen ist, wird eine Teststatistik berechnet. Die Entscheidung wird auf der Grundlage des numerischen Wertes der Teststatistik getroffen. Es gibt zwei Ansätze, um zu dieser Entscheidung zu gelangen: Der Ansatz des kritischen Wertes und der Ansatz des \(p\)-Wertes.

Der Ansatz des kritischen Wertes

Mit dem Ansatz des kritischen Wertes wird festgestellt, ob die beobachtete Teststatistik zu stark von einem definiertem kritischen Wert abweicht oder nicht. Dazu wird die beobachtete Teststatistik (berechnet auf der Grundlage der Stichprobendaten) mit dem kritischen Wert, einer Art Grenzwert, verglichen. Wenn die Teststatistik extremer ist als der kritische Wert, wird die Nullhypothese abgelehnt. Wenn die Teststatistik nicht so extrem ist wie der kritische Wert, wird die Nullhypothese nicht verworfen. Der kritische Wert wird auf der Grundlage des vorgegebenen Signifikanzniveaus \(\alpha\) und der Art der Wahrscheinlichkeitsverteilung des idealisierten Modells berechnet. Der kritische Wert teilt die Fläche unter der Wahrscheinlichkeitsverteilungskurve in die Ablehnungsregion(en) und in die Nichtablehnungsregion.

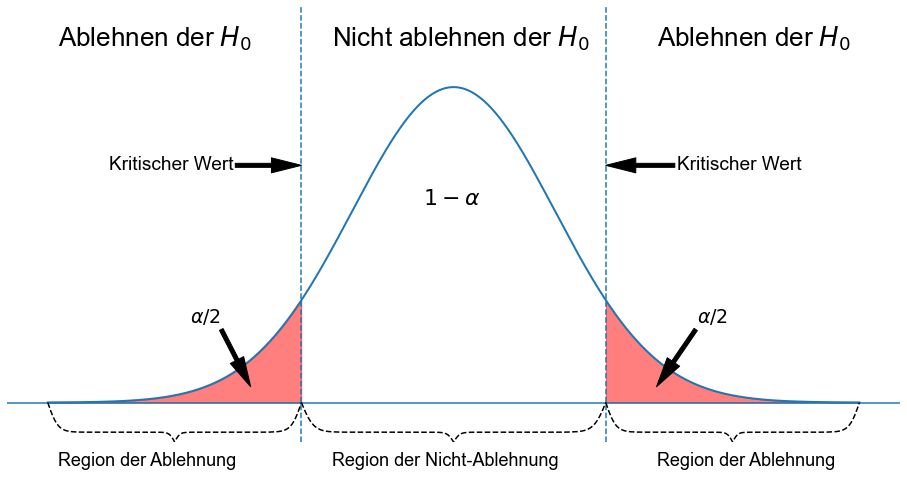
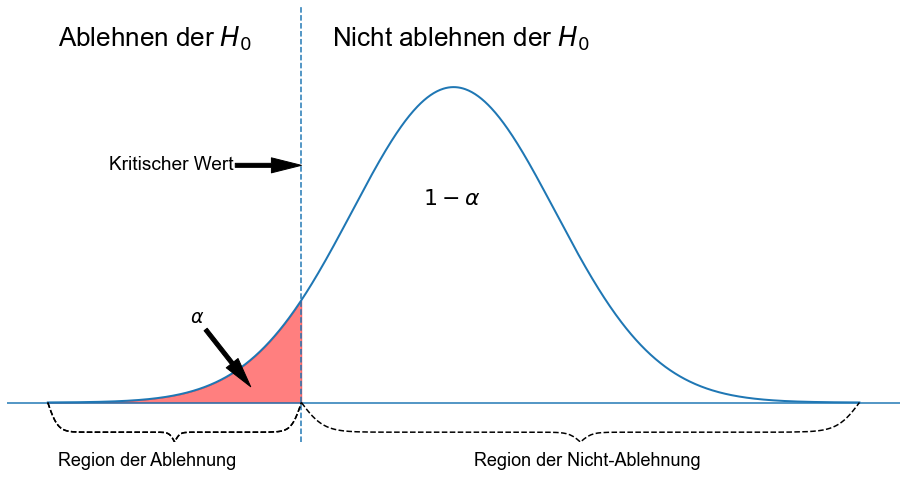
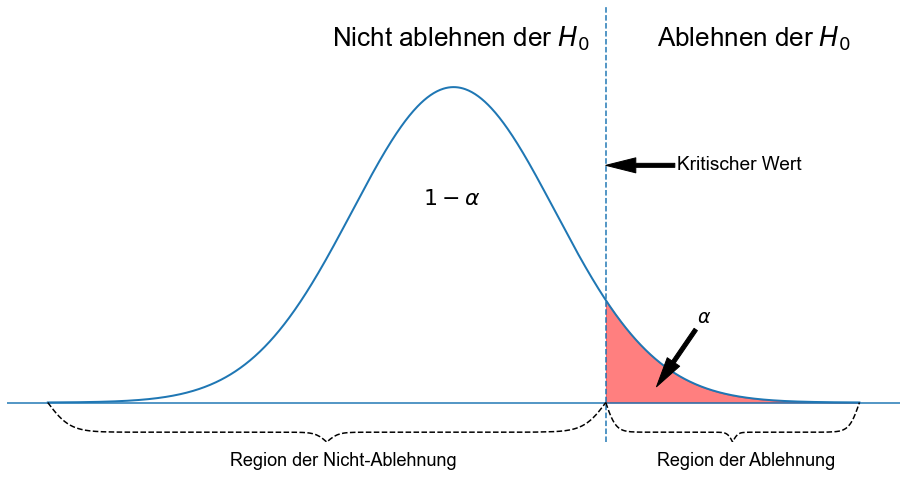
Die folgenden drei Abbildungen zeigen einen rechtsseitigen Test, einen linksseitigen Test und einen zweiseitigen Test. Das idealisierte Modell in den Abbildungen, und damit \(H_0\) wird durch eine glockenförmige normale Wahrscheinlichkeitskurve beschrieben.

Bei einem zweiseitigen Test wird die Nullhypothese abgelehnt, wenn die Teststatistik entweder zu klein oder zu groß ist. Der Ablehnungsbereich für einen solchen Test besteht also aus zwei Teilen: einem links und einem rechts.

import numpy as np


def range_brace(
    x_min,
    x_max,
    mid=0.75,
    beta1=50.0,
    beta2=100.0,
    height=1,
    initial_divisions=11,
    resolution_factor=1.5,
):
    # determine x0 adaptively values using second derivitive
    # could be replaced with less snazzy:
    #   x0 = np.arange(0, 0.5, .001)
    x0 = np.array(())
    tmpx = np.linspace(0, 0.5, initial_divisions)
    tmp = (
        beta1**2
        * (np.exp(beta1 * tmpx))
        * (1 - np.exp(beta1 * tmpx))
        / np.power((1 + np.exp(beta1 * tmpx)), 3)
    )
    tmp += (
        beta2**2
        * (np.exp(beta2 * (tmpx - 0.5)))
        * (1 - np.exp(beta2 * (tmpx - 0.5)))
        / np.power((1 + np.exp(beta2 * (tmpx - 0.5))), 3)
    )
    for i in range(0, len(tmpx) - 1):
        t = int(
            np.ceil(
                resolution_factor
                * max(np.abs(tmp[i : i + 2]))
                / float(initial_divisions)
            )
        )
        x0 = np.append(x0, np.linspace(tmpx[i], tmpx[i + 1], t))
    x0 = np.sort(np.unique(x0))  # sort and remove dups
    # half brace using sum of two logistic functions
    y0 = mid * 2 * ((1 / (1.0 + np.exp(-1 * beta1 * x0))) - 0.5)
    y0 += (1 - mid) * 2 * (1 / (1.0 + np.exp(-1 * beta2 * (x0 - 0.5))))
    # concat and scale x
    x = np.concatenate((x0, 1 - x0[::-1])) * float((x_max - x_min)) + x_min
    y = np.concatenate((y0, y0[::-1])) * float(height)
    return (x, y)

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(16, 8))
x_min = -4
x_max = 4
x = np.linspace(x_min, x_max, 1000)

mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=2)


ticks = [-1.5, 1.5]
for _x in ticks:
    ax.axvline(_x, linestyle="dashed")

ax.axhline(0)
ax.axis("off")

ax.fill_between(x, norm.pdf(x), where=x <= ticks[0], color="r", alpha=0.5)
ax.fill_between(x, norm.pdf(x), where=x >= ticks[1], color="r", alpha=0.5)

x, y = range_brace(
    ticks[0],
    ticks[1],
    height=0.05,
)
ax.plot(x, -y, "--", color="k")

x, y = range_brace(
    x_min,
    ticks[0],
    height=0.05,
)
ax.plot(x, -y, "--", color="k")

x, y = range_brace(
    ticks[1],
    x_max,
    height=0.05,
)
ax.plot(x, -y, "--", color="k")

ax.text(s="Ablehnen der $H_0$", x=-3.9, y=0.45, size=26)
ax.text(s="Ablehnen der $H_0$", x=2, y=0.45, size=26)
ax.text(s="Nicht ablehnen der $H_0$", x=-1.2, y=0.45, size=26)


ax.text(s="Region der Ablehnung", x=-3.9, y=-0.08, size=18)
ax.text(s="Region der Ablehnung", x=2, y=-0.08, size=18)
ax.text(s="Region der Nicht-Ablehnung", x=-1.2, y=-0.08, size=18)

ax.text(s=r"$1-\alpha$", x=-0.3, y=0.25, size=22)

ax.annotate(
    r"$\alpha/2$",
    xy=(2, 0.02),
    xytext=(2.4, 0.1),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
)

ax.annotate(
    r"$\alpha/2$",
    xy=(-2, 0.02),
    xytext=(-2.6, 0.1),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
)

ax.annotate(
    r"Kritischer Wert",
    xy=(ticks[1], 0.3),
    xytext=(2.2, 0.3),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
    verticalalignment="center",
)

ax.annotate(
    r"Kritischer Wert",
    xy=(ticks[0], 0.3),
    xytext=(-3.4, 0.3),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
    verticalalignment="center",
)

ax.set_ylim(-0.05, 0.5)

(-0.05, 0.5)

Bei einem linksseitigen Test wird die Nullhypothese abgelehnt, wenn die Teststatistik zu klein ist. Der Ablehnungsbereich für einen solchen Test besteht also aus einem Teil, der links von der Mitte liegt.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(16, 8))
x_min = -4
x_max = 4
x = np.linspace(x_min, x_max, 1000)

mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=2)


ticks = [-1.5]
for _x in ticks:
    ax.axvline(_x, linestyle="dashed")

ax.axhline(0)
ax.axis("off")

ax.fill_between(x, norm.pdf(x), where=x <= ticks[0], color="r", alpha=0.5)

x, y = range_brace(
    ticks[0],
    x_max,
    height=0.05,
)
ax.plot(x, -y, "--", color="k")

x, y = range_brace(
    x_min,
    ticks[0],
    height=0.05,
)
ax.plot(x, -y, "--", color="k")

ax.plot(x, -y, "--", color="k")

ax.text(s="Ablehnen der $H_0$", x=-3.9, y=0.45, size=26)
ax.text(s="Nicht ablehnen der $H_0$", x=-1.2, y=0.45, size=26)


ax.text(s="Region der Ablehnung", x=-3.9, y=-0.08, size=18)
ax.text(s="Region der Nicht-Ablehnung", x=0.2, y=-0.08, size=18)

ax.text(s=r"$1-\alpha$", x=-0.3, y=0.25, size=22)


ax.annotate(
    r"$\alpha$",
    xy=(-2, 0.02),
    xytext=(-2.6, 0.1),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
)


ax.annotate(
    r"Kritischer Wert",
    xy=(ticks[0], 0.3),
    xytext=(-3.4, 0.3),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
    verticalalignment="center",
)

ax.set_ylim(-0.05, 0.5)

(-0.05, 0.5)

Bei einem rechtsseitigen Test wird die Nullhypothese abgelehnt, wenn die Teststatistik zu groß ist. Der Ablehnungsbereich für einen solchen Test besteht also aus einem Teil, der sich rechts von der Mitte befindet.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(16, 8))
x_min = -4
x_max = 4
x = np.linspace(x_min, x_max, 1000)

mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=2)


ticks = [1.5]
for _x in ticks:
    ax.axvline(_x, linestyle="dashed")

ax.axhline(0)
ax.axis("off")

ax.fill_between(x, norm.pdf(x), where=x >= ticks[0], color="r", alpha=0.5)

x, y = range_brace(
    x_min,
    ticks[0],
    height=0.05,
)
ax.plot(x, -y, "--", color="k")


x, y = range_brace(
    ticks[0],
    x_max,
    height=0.05,
)
ax.plot(x, -y, "--", color="k")

ax.text(s="Ablehnen der $H_0$", x=2, y=0.45, size=26)
ax.text(s="Nicht ablehnen der $H_0$", x=-1.2, y=0.45, size=26)


ax.text(s="Region der Ablehnung", x=2, y=-0.08, size=18)
ax.text(s="Region der Nicht-Ablehnung", x=-2.2, y=-0.08, size=18)

ax.text(s=r"$1-\alpha$", x=-0.3, y=0.25, size=22)

ax.annotate(
    r"$\alpha$",
    xy=(2, 0.02),
    xytext=(2.4, 0.1),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
)

ax.annotate(
    r"Kritischer Wert",
    xy=(ticks[0], 0.3),
    xytext=(2.2, 0.3),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=19,
    verticalalignment="center",
)

ax.set_ylim(-0.05, 0.5)

(-0.05, 0.5)

Der \(p\)-Wert-Ansatz

Bei der \(p\)-Wert-Methode wird die Wahrscheinlichkeit (\(p\)-Wert) des numerischen Wertes der Teststatistik mit dem angegebenen Signifikanzniveau (\(\alpha\)) des Hypothesentests verglichen.

Der \(p\)-Wert entspricht der Wahrscheinlichkeit, Stichprobendaten zu beobachten, die mindestens so extrem sind wie die tatsächlich erhaltene Teststatistik. Kleine \(p\)-Werte sind ein Beweis gegen die Nullhypothese. Je kleiner (näher an \(0\)) der \(p\)-Wert ist, desto stärker ist der Beweis gegen die Nullhypothese.

Ist der \(p\)-Wert kleiner als oder gleich dem angegebenen Signifikanzniveau \(\alpha\) ist, wird die Nullhypothese abgelehnt; andernfalls wird die Nullhypothese nicht abgelehnt. Mit anderen Worten: wenn \(p \le \alpha\), wird \(H_0\) abgelehnt; andernfalls, wenn \(p \gt \alpha\), wird \(H_0\) nicht abgelehnt.

Folglich kann durch die Kenntnis des \(p\)-Wertes jedes gewünschte Signifikanzniveau bewertet werden. Beträgt der \(p\)-Wert eines Hypothesentests beispielsweise \(0,01\), kann die Nullhypothese auf jedem Signifikanzniveau größer oder gleich \(0,01\) abgelehnt werden. Bei einem Signifikanzniveau kleiner als \(0,01\) wird sie nicht verworfen. Daher wird der \(p\)-Wert in der Regel verwendet, um die Stärke des Beweises gegen die Nullhypothese ohne Bezug auf das Signifikanzniveau zu bewerten.

Die folgende Tabelle enthält Leitlinien für die Verwendung des \(p\)-Werts zur Bewertung der Beweise gegen die Nullhypothese (Fahrmeir et al. [2016] s.388).

\[\begin{split} \begin{array}{l|l} \hline \text{$p$-Wert} & \text{Hinweise gegen } H_0 \\ \hline \ p > 0,10 & \text{Schwache oder keine Hinweise } \\ \ 0,05 < p \le 0,10 & \text{Mäßiger Hinweis } \\ \ 0,01 < p \le 0,05 & \text{Starker Hinweis} \\ \ p \le 0,01 & \text{Sehr starker Hinweis} \\ \hline \end{array} \end{split}\]

previous

Lernziele

next

Hypothesentests für den Mittelwert einer Grundgesamtheit