Die F-Verteilung
Contents
Die F-Verteilung¶
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import f
Die Snedecor-\(F\)-Verteilung oder die Fisher-Snedecor-Verteilung (nach Sir Ronald A. Fisher und George W. Snedecor) oder kurz die \(F\)-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung mit dem Bereich \([0 \ \),\( \ +\infty[\), abhängig von zwei Parametern, die mit \(v_1,v_2\) bezeichnet werden ([Fahrmeir et al., 2016] s.281, [Scheid, 2021] s.179). In statistischen Anwendungen sind \(v_1,v_2\) positive ganze Zahlen.
Seien \(Y_1\) und \(Y_2\) seien zwei unabhängige Zufallsvariablen, die Chi-Quadrat-verteilt sind, mit \(v_1\) bzw. \(v_2\) Freiheitsgraden. Dann wird die Verteilung des Verhältnisses (\(Z\))
als \(F\)-Verteilung mit \(v_1\) und \(v_2\) Freiheitsgraden bezeichnet. Die \(F\)-Verteilung wird häufig auch als Verteilung des Varianzverhältnisses bezeichnet ([Fahrmeir et al., 2016] s.281).
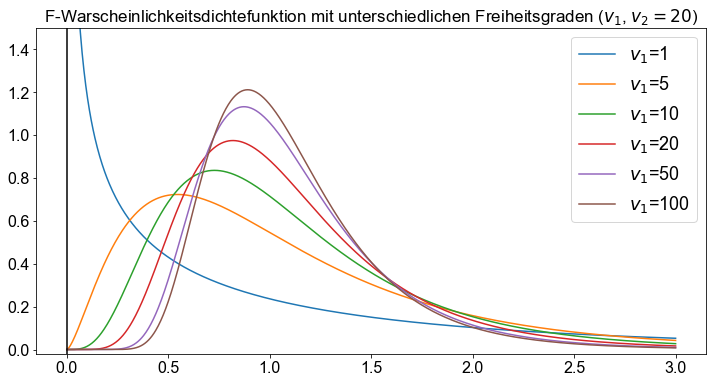
Eine \(F\)-Verteilung hat zwei Zahlen von Freiheitsgraden, \(v_1\) und \(v_2\), die ihre Form bestimmen. Die erste Zahl der Freiheitsgrade, \(v_1\), wird als die Freiheitsgrade des Zählers und die zweite, \(v_2\), als die Freiheitsgrade des Nenners bezeichnet.
from scipy.stats import f
import numpy as np
import matplotlib.pyplot as plt
v1 = [1, 5, 10, 20, 50, 100]
v2 = 20
x = np.linspace(0, 3, 1000)
fig, ax = plt.subplots()
for _df in v1:
ax.plot(x, f.pdf(x, dfn=_df, dfd=v2), label=f"$v_1$={_df}")
ax.set_title(
"F-Warscheinlichkeitsdichtefunktion mit unterschiedlichen Freiheitsgraden ($v_1$, $v_2 =20$)"
)
ax.legend(fontsize=18)
ax.set_ylim(-0.02, 1.5)
ax.axvline(0, color="k")
<matplotlib.lines.Line2D at 0x16ca8bee0>
from scipy.stats import f
import numpy as np
import matplotlib.pyplot as plt
v1 = 20
v2 = [1, 5, 10, 20, 50, 100]
x = np.linspace(0, 3, 1000)
fig, ax = plt.subplots()
for _df in v2:
ax.plot(x, f.pdf(x, dfn=v1, dfd=_df), label=f"$v_1$={_df}")
ax.set_title(
"F-Warscheinlichkeitsdichtefunktion mit unterschiedlichen Freiheitsgraden ($v_1=20$, $v_2$)"
)
ax.legend(fontsize=18)
ax.set_ylim(-0.02, 1.5)
ax.axvline(0, color="k")
<matplotlib.lines.Line2D at 0x16d3c3e20>
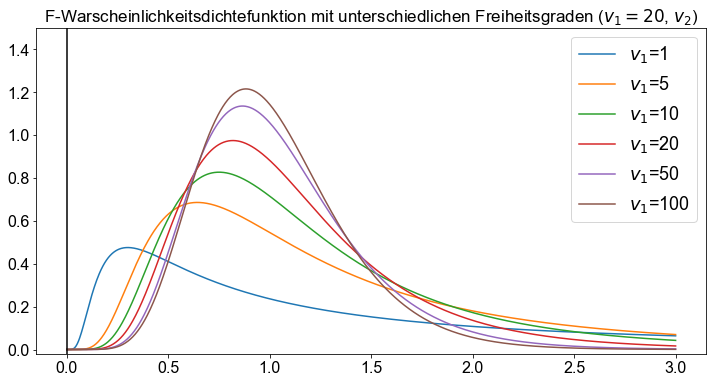
Grundlegende Eigenschaften von F-Kurven
Die Gesamtfläche unter einer \(F\)-Kurve ist gleich \(1\). -Eine \(F\)-Kurve beginnt bei \(0\) auf der horizontalen Achse und erstreckt sich unendlich weit nach rechts, wobei sie sich der horizontalen Achse nähert, diese aber nie berührt.
Eine \(F\)-Kurve ist rechtsschief.
Die F-Verteilung in Python¶
Die wichtigsten Funktionen zur Interaktion mit der \(F\)-Verteilung sind f.pdf(), f.cdf(), f.ppf(), f.rvs(). Die Funktion f.pdf() liefert die Dichte, die Funktion f.cdf() die Verteilungsfunktion, die Funktion f.ppf() die Quantilfunktion und die Funktion f.rvs() erzeugt Zufallsabweichungen.
Wir verwenden die Funktion f.pdf(), um die Dichte bei einem Wert von \(1,2\) einer \(F\)-Kurve mit \(v_1=10\) und \(v_2=20\).
f.pdf(1.2, 10, 20)
0.5626124566227062
Wir verwenden f.cdf(), um die Fläche unter der Kurve für das Intervall \([0 \ \),\( \ 1,5]\) und das Intervall \([1,5 \ \),\( \ +\infty[\) einer F-Kurve mit \(v_1=10\) und \(v_2=20\) zu berechnen. Weiter fragen wir Python, ob die Summe der Intervalle \([0 \ \),\( \ 1,5]\) und \([1,5 \ \),\( \ +\infty[\) den Wert \(1\) ergibt.
f_cdf1 = f.cdf(1.5, 10, 20)
f_cdf1
0.7890535374813874
f_cdf2 = 1 - f.cdf(1.5, 10, 20)
f_cdf2
0.2109464625186126
f_cdf1 + f_cdf2
1.0
Wir verwenden f.ppf(), um das Quantil für eine bestimmte Fläche (= Wahrscheinlichkeit) unter der Kurve für eine \(F\)-Kurve mit \(v_1=10\) und \(v_2=20\) zu berechnen, die \(q=0,25,0,5,0,75\) und \(0,999\) entspricht.
q = [0.25, 0.5, 0.75, 0.999]
f.ppf(q, 10, 20)
array([0.65639363, 0.96626389, 1.39948744, 5.07524621])
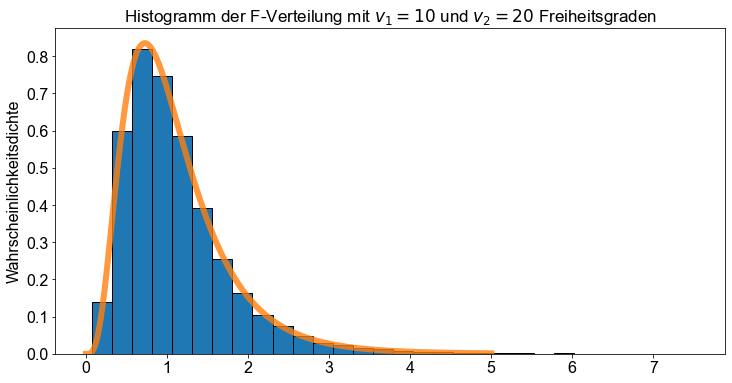
Wir verwenden die Funktion f.rvs(), um \(100.000\) Zufallswerte aus der \(F\)-Verteilung mit \(v_1=10\) und \(v_2=20\) zu erzeugen. Anschließend zeichnen wir ein Histogramm und vergleichen es mit der Wahrscheinlichkeitsdichtefunktion der \(F\)-Verteilung mit \(v_1=10\) und \(v_2=20\) (orange Linie).
# Erzeuge Chi^2 Werte
f_rvs = f.rvs(10, 20, size=10000)
# Erzeuge x-werte
x = np.linspace(0, 5, num=1000)
# Plotte t-Verteilung
fig, ax = plt.subplots()
# plt.xlim(0,4.5)
ax.set_title("Histogramm der F-Verteilung mit $v_1=10$ und $v_2=20$ Freiheitsgraden")
ax.set_ylabel("Wahrscheinlichkeitsdichte")
ax.hist(f_rvs, bins=30, edgecolor="k", density=True)
ax.plot(x, f.pdf(x, 10, 20), linewidth=6, alpha=0.8)
[<matplotlib.lines.Line2D at 0x16d49b3d0>]