Die Normalverteilung
Contents
Die Normalverteilung¶
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import norm
import statsmodels.api as smi
Die Normalverteilung wird in der Wahrscheinlichkeitstheorie, der Statistik sowie in den Natur- und Sozialwissenschaften häufig verwendet. Sie wird auch Gauß-Verteilung genannt, weil Carl Friedrich Gauß \((1777-1855)\) einer der ersten war, der sie für die Analyse astronomischer Daten verwendete (Fahrmeir et al. [2016] s.83,s.271).
Die Normalverteilung oder die Normalkurve ist eine glockenförmige (symmetrische) Kurve. Ihr Mittelwert wird mit \(\mu\) und ihre Standardabweichung mit \(\sigma\) bezeichnet. Eine kontinuierliche Zufallsvariable \(x\), die eine Normalverteilung aufweist, wird als normale Zufallsvariable bezeichnet.
Die Notation für eine Normalverteilung lautet \(X \sim N( \mu, \sigma)\). Die Wahrscheinlichkeitsdichtefunktion (PDF) wird geschrieben als
wobei \(e \approx 2,71828\) und \(\pi \approx 3,14159\). Die Wahrscheinlichkeitsdichtefunktion \(f(x)\) gibt den vertikalen Abstand zwischen der horizontalen Achse und der Normalkurve im Punkt \(x\) an.
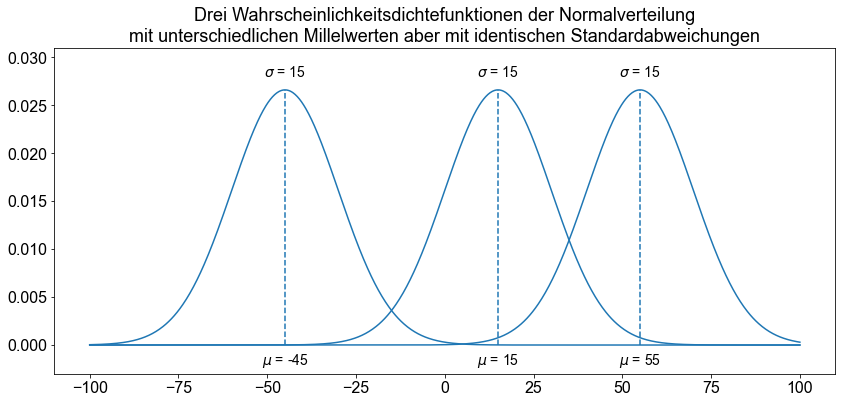
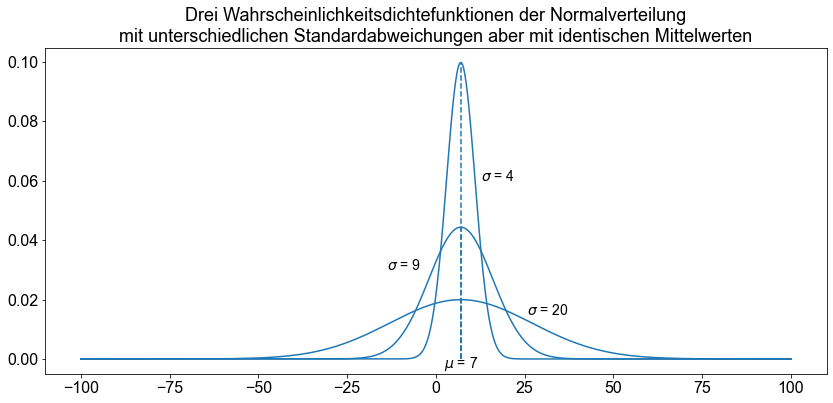
Die Normalverteilung wird durch zwei Parameter beschrieben, den Mittelwert \(\mu\) und die Standardabweichung \(\sigma\). Jeder unterschiedliche Satz von Werten für \(\mu\) und \(\sigma\) ergibt eine andere Normalverteilung. Der Wert von \(\mu\) bestimmt den Mittelpunkt einer Normalverteilungskurve auf der horizontalen Achse, und der Wert von \(\sigma\) gibt die Streuung der Werte um den Mittelpunkt an.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(14, 6))
x = np.linspace(-100, 100, 1000)
sigma = 15
mu = -45
ax.plot(x, norm.pdf(x, mu, sigma), color="C0")
ax.vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax.text(mu, -0.002, s=f"$\mu$ = {mu}", horizontalalignment="center", size=14)
ax.text(
mu,
norm.pdf(mu, mu, sigma) * 1.05,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=14,
)
mu = 15
ax.plot(x, norm.pdf(x, mu, sigma), color="C0")
ax.vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax.text(mu, -0.002, s=f"$\mu$ = {mu}", horizontalalignment="center", size=14)
ax.text(
mu,
norm.pdf(mu, mu, sigma) * 1.05,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=14,
)
mu = 55
ax.plot(x, norm.pdf(x, mu, sigma), color="C0")
ax.vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax.text(mu, -0.002, s=f"$\mu$ = {mu}", horizontalalignment="center", size=14)
ax.text(
mu,
norm.pdf(mu, mu, sigma) * 1.05,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=14,
)
ax.set_title(
"Drei Wahrscheinlichkeitsdichtefunktionen der Normalverteilung\nmit unterschiedlichen Millelwerten aber mit identischen Standardabweichungen",
size=18,
)
ax.set_ylim(-0.003, 0.031)
(-0.003, 0.031)
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(14, 6))
x = np.linspace(-100, 100, 1000)
mu = 7
ax.text(mu, -0.003, s=f"$\mu$ = {mu}", horizontalalignment="center", size=14)
sigma = 4
ax.plot(x, norm.pdf(x, mu, sigma), color="C0")
ax.vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax.text(mu * 2.5, 0.06, s=f"$\sigma$ = {sigma}", horizontalalignment="center", size=14)
sigma = 9
ax.plot(x, norm.pdf(x, mu, sigma), color="C0")
ax.vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax.text(mu * -1.3, 0.03, s=f"$\sigma$ = {sigma}", horizontalalignment="center", size=14)
sigma = 20
ax.plot(x, norm.pdf(x, mu, sigma), color="C0")
ax.vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax.text(mu * 4.5, 0.015, s=f"$\sigma$ = {sigma}", horizontalalignment="center", size=14)
ax.set_title(
"Drei Wahrscheinlichkeitsdichtefunktionen der Normalverteilung\nmit unterschiedlichen Standardabweichungen aber mit identischen Mittelwerten",
size=18,
)
Text(0.5, 1.0, 'Drei Wahrscheinlichkeitsdichtefunktionen der Normalverteilung\nmit unterschiedlichen Standardabweichungen aber mit identischen Mittelwerten')
Eine Normalverteilung ist unter anderem durch die folgenden Merkmale gekennzeichnet (Fahrmeir et al. [2016] s.272):
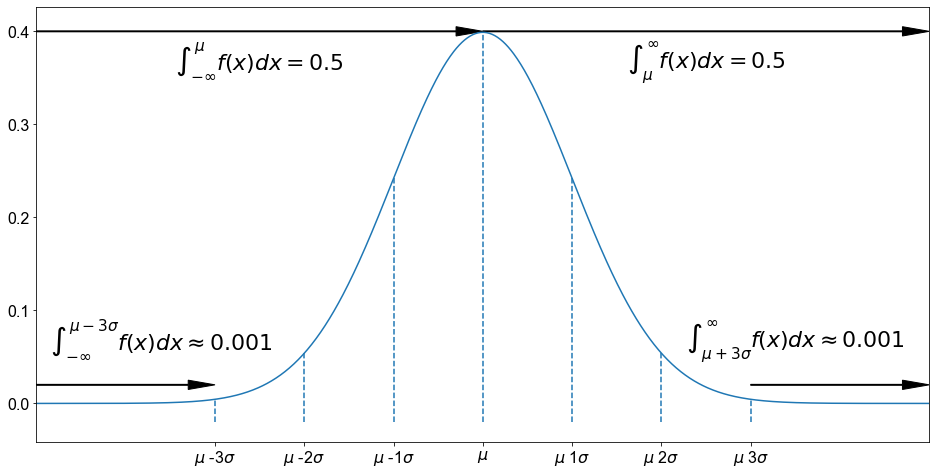
Die Gesamtfläche unter einer Normalverteilungskurve beträgt \(1,0\), also \(100 \%\).
Eine Normalverteilungskurve ist symmetrisch um den Mittelwert. Folglich liegen \(50 \%\) der Gesamtfläche unter einer Normalverteilungskurve auf der linken Seite des Mittelwerts und \(50 \%\) liegen auf der rechten Seite des Mittelwerts.
Die Ausläufer einer Normalverteilungskurve erstrecken sich unendlich weit in beide Richtungen, ohne die horizontale Achse zu berühren oder zu kreuzen. Obwohl eine Normalverteilungskurve niemals die horizontale Achse berührt, kommt sie jenseits der Punkte, durch \(\mu-3\sigma\) und \(\mu+3\sigma\) dargestellten Punkte so nahe an diese Achse heran, dass die Fläche unter der Kurve jenseits dieser Punkte in beiden Richtungen praktisch als Null angenommen werden kann.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-5, 5, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0")
x = [-3, -2, -1, 0, 1, 2, 3]
for _x in x:
ax.vlines(_x, ymin=-0.02, ymax=norm.pdf(_x, mu, sigma), linestyle="dashed")
ax.set_xticks(x)
ax.set_xticklabels([f"$\mu$ {x}$\sigma$" if x != 0 else f"$\mu$" for x in x])
ax.text(
-3.6,
0.06,
s=r"$\int_{-\infty}^{\mu-3\sigma} f(x)dx \approx 0.001$",
horizontalalignment="center",
size=22,
)
ax.arrow(-5, 0.02, 1.7, 0, head_width=0.01, head_length=0.3, color="k")
ax.text(
-2.5,
0.36,
s="$\int_{-\infty}^\mu f(x)dx=0.5$",
horizontalalignment="center",
size=22,
)
ax.arrow(-5, 0.4, 4.7, 0, head_width=0.01, head_length=0.3, color="k")
ax.text(
2.5,
0.36,
s="$\int_\mu^\infty f(x)dx=0.5$",
horizontalalignment="center",
size=22,
)
ax.arrow(0, 0.4, 4.7, 0, head_width=0.01, head_length=0.3, color="k")
ax.text(
3.5,
0.06,
s=r"$\int_{\mu+3\sigma}^\infty f(x)dx \approx 0.001$",
horizontalalignment="center",
size=22,
)
ax.arrow(3, 0.02, 1.7, 0, head_width=0.01, head_length=0.3, color="k")
ax.set_xlim(-5, 5)
(-5.0, 5.0)
Die Standard-Normalverteilung¶
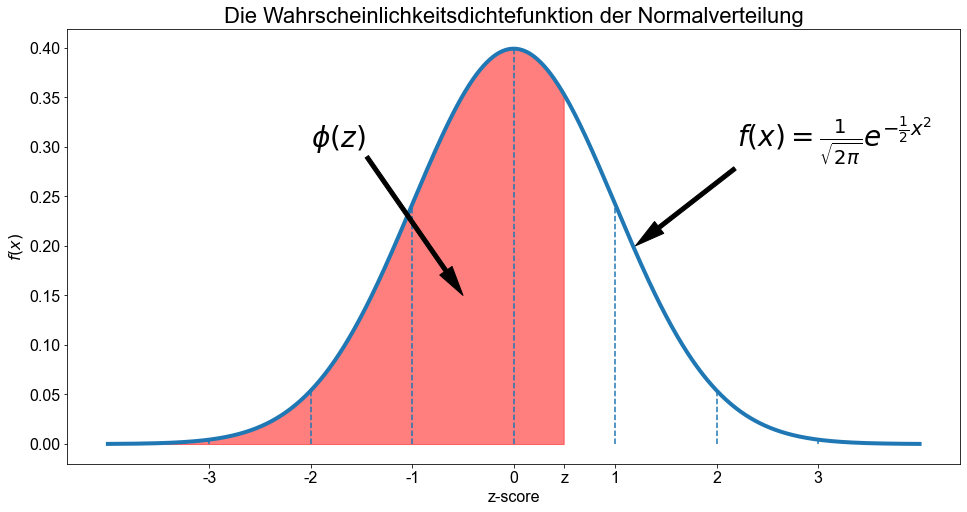
Die Standardnormalverteilung ist ein Spezialfall der Normalverteilung. Bei der Standardnormalverteilung ist der Wert des Mittelwerts gleich Null \((\mu=0)\) und der Wert der Standardabweichung gleich \(1\) \((\sigma=1)\).
Wenn man also \(\mu =0\) und \(\sigma =1\) in die PDF der Normalverteilung einsetzt, vereinfacht sich die Gleichung zu
Die Zufallsvariable, die die Standardnormalverteilung erfüllt, wird mit \(z\) bezeichnet. Folglich werden die Einheiten für die Kurve der Standardnormalverteilung mit \(z\) bezeichnet und als \(z\)-Werte, \(z\)-Scores oder \(z\)-Statistik bezeichnet.
Die kumulative Verteilungsfunktion (CDF) der Standardnormalverteilung, die der Fläche unter der Kurve für das Intervall \(]-\infty \ \),\( \ z]\) entspricht und gewöhnlich mit dem griechischen Großbuchstaben \(\phi\) bezeichnet wird, ist gegeben durch
wobei \(e \approx 2,71828\) und \(\pi \approx 3,14159\).
Grundlegende Eigenschaften der Standardnormalkurve¶
Die Standardnormalkurve ist ein Spezialfall der Normalverteilung und damit auch eine Wahrscheinlichkeitsverteilungskurve. Daher gelten die grundlegenden Eigenschaften der Normalverteilung auch für die Standardnormalkurve (Fahrmeir et al. [2016] s.85).
Die Gesamtfläche unter der Standardnormalkurve ist \(1\) (diese Eigenschaft ist allen Dichtekurven gemeinsam).
Die Standardnormalkurve erstreckt sich unendlich in beide Richtungen und nähert sich dabei der horizontalen Achse, berührt sie aber nie.
Die Standardnormalkurve ist glockenförmig, ihr Mittelpunkt liegt bei \(z=0\). Fast die gesamte Fläche unter der Standardnormalkurve liegt zwischen \(z=-3\) und \(z=3\).
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=4)
z = 0.5
ticks = [-3, -2, -1, 0, z, 1, 2, 3]
for _x in ticks:
if _x != z:
ax.vlines(_x, ymin=-0, ymax=norm.pdf(_x, mu, sigma), linestyle="dashed")
ax.set_xticks(ticks)
ax.set_xticklabels(["z" if x == z else str(x) for x in ticks])
ax.fill_between(x, norm.pdf(x), where=x <= z, color="r", alpha=0.5)
ax.set_ylabel(r"$f(x)$")
ax.set_xlabel(r"z-score")
ax.annotate(
r"$\phi(z)$",
xy=(-0.5, 0.15),
xytext=(-2, 0.3),
# textcoords="data",
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=28,
)
ax.annotate(
r"$f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}x^2}$",
xy=(1.2, 0.2),
xytext=(2.2, 0.3),
# textcoords="data",
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=28,
)
ax.set_title("Die Wahrscheinlichkeitsdichtefunktion der Normalverteilung", size=22)
Text(0.5, 1.0, 'Die Wahrscheinlichkeitsdichtefunktion der Normalverteilung')
Die \(z\)-Werte auf der rechten Seite des Mittelwerts sind positiv und die auf der linken Seite sind negativ. Der \(z\)-Wert für einen Punkt auf der horizontalen Achse gibt den Abstand zwischen dem Mittelwert \((z=0)\) und diesem Punkt in Form der Standardabweichung an. Ein Punkt mit einem Wert von \(z=2\) liegt zum Beispiel zwei Standardabweichungen rechts vom Mittelwert. Ebenso liegt ein Punkt mit einem Wert von \(z=-2\) zwei Standardabweichungen links vom Mittelwert.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.cdf(x), color="C0", linewidth=4)
z = 0.5
ticks = [-3, -2, -1, 0, z, 1, 2, 3]
for _x in ticks:
if _x != z:
ax.vlines(_x, ymin=-0, ymax=norm.cdf(_x, mu, sigma), linestyle="dashed")
ax.set_xticks(ticks)
ax.set_xticklabels(["z" if x == z else str(x) for x in ticks])
ax.fill_between(x, norm.cdf(x), where=x <= z, color="r", alpha=0.5)
ax.set_ylabel(r"$f(x)$")
ax.set_xlabel(r"z-score")
ax.annotate(
r"$\phi(z) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^ze^{-\frac{1}{2}x^2}dx$",
xy=(-0.2, 0.2),
xytext=(-4, 0.7),
# textcoords="data",
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=28,
)
ax.set_title(
"Die kumulative Wahrscheinlichkeitsdichtefunktion der Normalverteilung", size=22
)
Text(0.5, 1.0, 'Die kumulative Wahrscheinlichkeitsdichtefunktion der Normalverteilung')
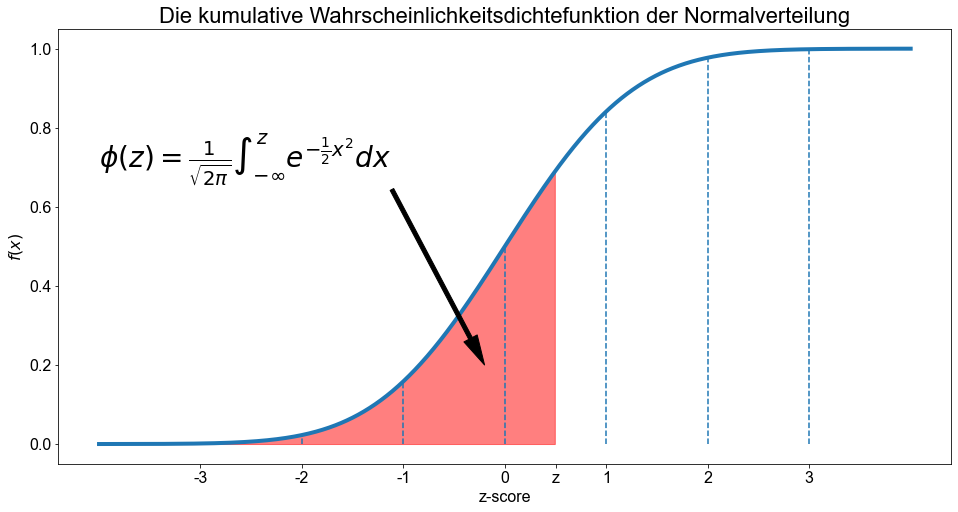
Das Methode die Wahrscheinlichkeiten durch Berechnung der Fläche unter der Standardnormalkurve zu bestimmen, kommt häufig zur Anwendung. Aus diesem Grund gibt es Wahrscheinlichkeitstabellen, um die Fläche für einen bestimmten \(z\)-Wert zu ermitteln. Python ist jedoch ein so leistungsfähiges Werkzeug, dass wir die Fläche unter der Kurve für einen bestimmten \(z\)-Wert berechnen können.
Um die Fläche unter der Kurve für eine Standardnormalverteilung zu berechnen, verwenden wir zunächst die Funktion norm aus dem scipy.stats Paket um eine Standardnormalverteilung zu generieren und wenden darauf die Methode cdf an um die kumulative Wahrscheinlichkeit zu berechnen. Die Funktion norm ist definiert als norm(loc = Mittelwert , scale = Standardabweichung). Um die Standardwerte zu Erhalten setzen wir den Mittelwert und die Standardabweichung jeweils auf \(0\) und \(1\) sind. Wenden wir die Methode cdf an bekommen wir die kumulative Wahrscheinlichkeit bis zum angegebenen Punkt. Wir berechnen die Fläche unter der Kurve für \(z=-3,-2,-1,0,1,2,3\) oder formeller geschrieben:
norm.cdf(-3)
0.0013498980316300933
norm.cdf(-2)
0.022750131948179195
norm.cdf(-1)
0.15865525393145707
norm.cdf(0)
0.5
norm.cdf(1)
0.8413447460685429
norm.cdf(2)
0.9772498680518208
norm.cdf(3)
0.9986501019683699
Perfekt! Wir haben einige der oben genannten Eigenschaften einer Standardnormalkurve bestätigt. Wir erinnern uns, dass wir die Fläche unter der Kurve für das Intervall \(]-\infty \ \),\( \ z]\) berechnet haben. Der Aufruf von norm.cdf(-3) ergibt eine sehr geringe Zahl. Nur etwa \(0,1 \%\) der gesamten Fläche unter der Kurve befinden sich links von \(z=-3\), was dem Abstand der dreifachen Standardabweichung vom Mittelwert entspricht. Außerdem ergibt norm.cdf(0) \(50 \%\). Fantastisch! Daraus schließen wir, dass die Fläche unter der Kurve für das Intervall \(]-\infty \ \),\( \ 0]\) die gleiche ist wie die Fläche unter der Kurve für das Intervall \([0 \ \),\( \ \infty[\) und dass die Fläche unter der Kurve sich zu \(1\) aufsummiert. Auch hier haben wir eine der oben genannten Eigenschaften einer Standardnormalkurve bestätigt. Und schließlich ergibt der Aufruf von norm.cdf(3) eine hohe Zahl nahe bei \(1\). Somit sind etwa \(99,9 \%\) der Fläche unter der Kurve im Intervall \(]-\infty \ \),\( \ 3]\) zu finden. Für den Bereich jenseits von \(z=3\) bleibt nur wenig übrig.
Es sei daran erinnert, dass wir die Fläche unter der Kurve für jedes beliebige Intervall explizit berechnen können
\( P(a \le z \le b) = P(z \le b) - P(z \le a) \)
\( =\int_{a}^{b}f(z)dz\)
\( = \int_{-\infty}^{b}f(x)dx - \int_{-\infty}^{a}f(x)dx \)
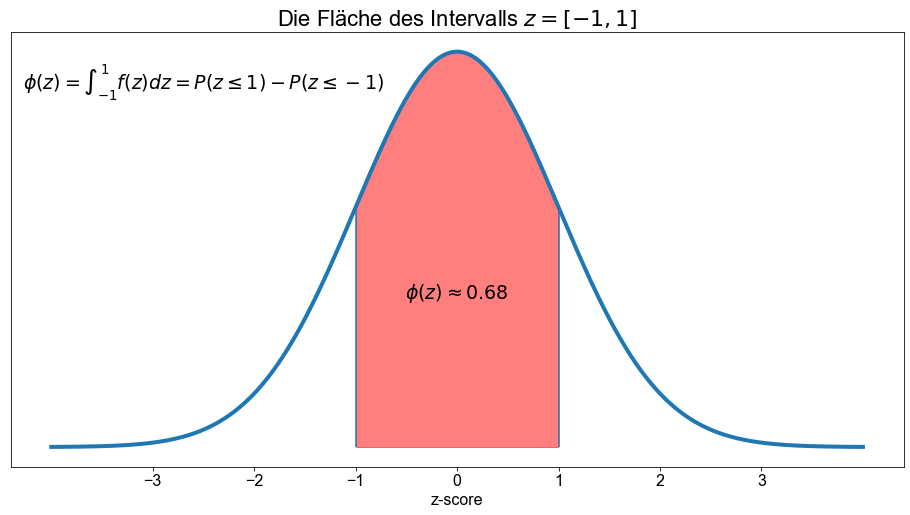
Berechnen wir die Fläche unter der Kurve für die folgenden Intervalle: \([−1 \ \),\( \ 1],[−2 \ \),\( \ 2],[−3 \ \),\( \ 3]\). Oder in Worten: Bestimmen wir die Fläche unter der Kurve für \(±1\) Standardabweichung, für \(±2\) Standardabweichungen und für \(±3\) Standardabweichungen.
norm.cdf(1) - norm.cdf(-1)
0.6826894921370859
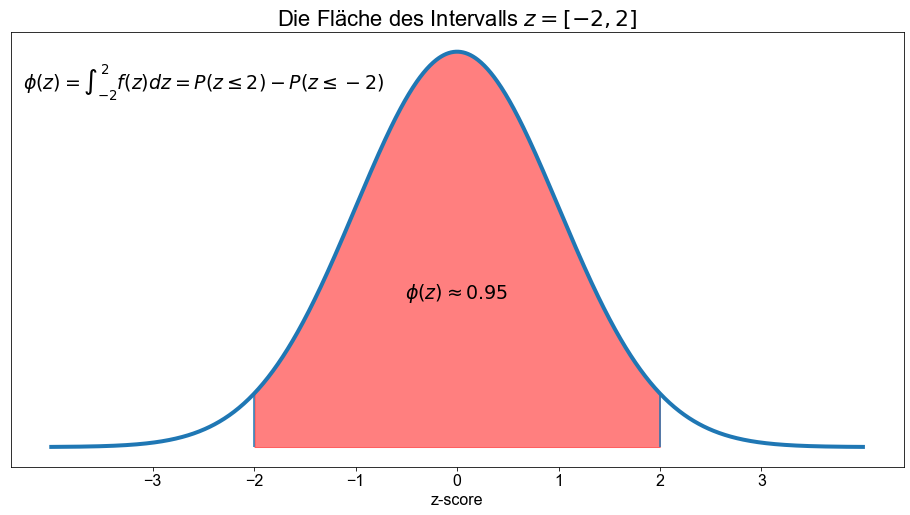
norm.cdf(2) - norm.cdf(-2)
0.9544997361036416
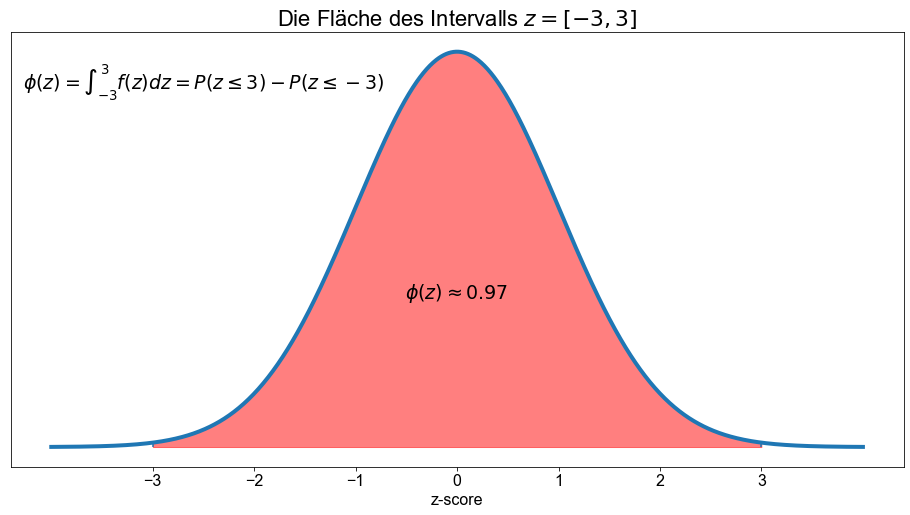
norm.cdf(3) - norm.cdf(-3)
0.9973002039367398
Toll, wir haben soeben die Empirische Regel (Fahrmeir et al. [2016] s.86), auch bekannt als \(68-95-99,7\)-Regel, bestätigt, die sich auf den Tschebyscheffsche Ungleichung bezieht. Für eine glockenförmige Verteilung sind die \(3\) Regeln dass ungefähr
\(68 \%\) der Beobachtungen liegen innerhalb einer Standardabweichung des Mittelwerts,
\(95 \%\) der Beobachtungen liegen innerhalb von zwei Standardabweichungen des Mittelwerts, und
\(99,7 \%\) der Beobachtungen liegen innerhalb von drei Standardabweichungen des Mittelwerts.
Um unsere Intuition zu stärken, wird die empirische Regel im Folgenden veranschaulicht.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=4)
for _x in [-1, 1]:
ax.vlines(_x, ymin=-0, ymax=norm.pdf(_x, mu, sigma))
ticks = [-3, -2, -1, 0, 1, 2, 3]
ax.set_xticks(ticks)
ax.fill_between(x, norm.pdf(x), where=(x >= -1) & (x <= 1), color="r", alpha=0.5)
ax.text(
-2.5,
0.36,
s="$\phi(z) = \int_{-1}^1 f(z)dz=P(z \leq 1) - P(z \leq-1)$",
horizontalalignment="center",
size=19,
)
ax.text(
0,
0.15,
s=r"$\phi(z) \approx 0.68$",
horizontalalignment="center",
size=19,
)
ax.set_xlabel(r"z-score")
ax.set_yticks([])
ax.set_title(r"Die Fläche des Intervalls $z=[-1,1]$", size=22)
Text(0.5, 1.0, 'Die Fläche des Intervalls $z=[-1,1]$')
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=4)
for _x in [-2, 2]:
ax.vlines(_x, ymin=-0, ymax=norm.pdf(_x, mu, sigma))
ticks = [-3, -2, -1, 0, 1, 2, 3]
ax.set_xticks(ticks)
ax.fill_between(x, norm.pdf(x), where=(x >= -2) & (x <= 2), color="r", alpha=0.5)
ax.text(
-2.5,
0.36,
s="$\phi(z) = \int_{-2}^2 f(z)dz=P(z \leq 2) - P(z \leq-2)$",
horizontalalignment="center",
size=19,
)
ax.text(
0,
0.15,
s=r"$\phi(z) \approx 0.95$",
horizontalalignment="center",
size=19,
)
ax.set_xlabel(r"z-score")
ax.set_yticks([])
ax.set_title(r"Die Fläche des Intervalls $z=[-2,2]$", size=22)
Text(0.5, 1.0, 'Die Fläche des Intervalls $z=[-2,2]$')
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=4)
for _x in [-3, 3]:
ax.vlines(_x, ymin=-0, ymax=norm.pdf(_x, mu, sigma))
ticks = [-3, -2, -1, 0, 1, 2, 3]
ax.set_xticks(ticks)
ax.fill_between(x, norm.pdf(x), where=(x >= -3) & (x <= 3), color="r", alpha=0.5)
ax.text(
-2.5,
0.36,
s="$\phi(z) = \int_{-3}^3 f(z)dz=P(z \leq 3) - P(z \leq-3)$",
horizontalalignment="center",
size=19,
)
ax.text(
0,
0.15,
s=r"$\phi(z) \approx 0.97$",
horizontalalignment="center",
size=19,
)
ax.set_xlabel(r"z-score")
ax.set_yticks([])
ax.set_title(r"Die Fläche des Intervalls $z=[-3,3]$", size=22)
Text(0.5, 1.0, 'Die Fläche des Intervalls $z=[-3,3]$')
Bestimmung des z-Wertes, bei bekannter Fläche unter der Normalverteilungskurve¶
Bisher haben wir \(z\)-Scores verwendet, um die Fläche unter der Kurve zu berechnen. Jetzt machen wir es andersherum. Wir berechnen den oder die \(z\)-Score(s), die einer bestimmten Fläche unter der Standardnormalkurve entsprechen. Das Auffinden des \(z\)-Scores, der eine bestimmte Fläche hat, ist so häufig, dass es eine spezielle Notation gibt. Das Symbol \(z_{\alpha}\) wird verwendet, um den \(z\)-Score zu bezeichnen, der eine Fläche von \( \alpha \) (alpha) zu seiner Rechten unter der Standardnormalkurve aufweist.
Ermitteln wir \(z_{0,05}\), den \(z\)-Wert, der unter der Standardnormalkurve eine Fläche von \(0,05\) zu seiner Rechten hat. Der Wert von \(\alpha\) entspricht der Wahrscheinlichkeit, einen bestimmten Wert zu erhalten, der dem Intervall \([z \ \),\( \ \infty[\)entspricht. Denn die Fläche rechts davon ist \(0,05\). Die Fläche links davon ist \(1-0,05=0,95\), was dem Intervall \(]- \alpha \ \),\( \ z]\) (siehe Grafik unten).
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=4)
for _x in [norm.ppf(0.95)]:
ax.vlines(_x, ymin=-0, ymax=norm.pdf(_x, mu, sigma))
z = norm.ppf(0.95)
ticks = [-3, -2, -1, 0, 1, z, 2, 3]
ax.set_xticks(ticks)
ax.set_xticklabels([np.round(x, 2) if x == z else x for x in ticks])
ax.fill_between(x, norm.pdf(x), where=(x >= norm.ppf(0.95)), color="r", alpha=0.5)
ax.text(
0,
0.15,
s=r"$Fläche = 0.95$",
horizontalalignment="center",
size=19,
)
ax.text(
1.85,
0.11,
s=r"$z_{0.05}$",
horizontalalignment="center",
size=19,
)
ax.annotate(
r"$Fläche=0.05$",
xy=(2, 0.02),
xytext=(2.4, 0.1),
# textcoords="data",
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=19,
)
ax.set_xlabel(r"z-score")
ax.set_yticks([])
[]
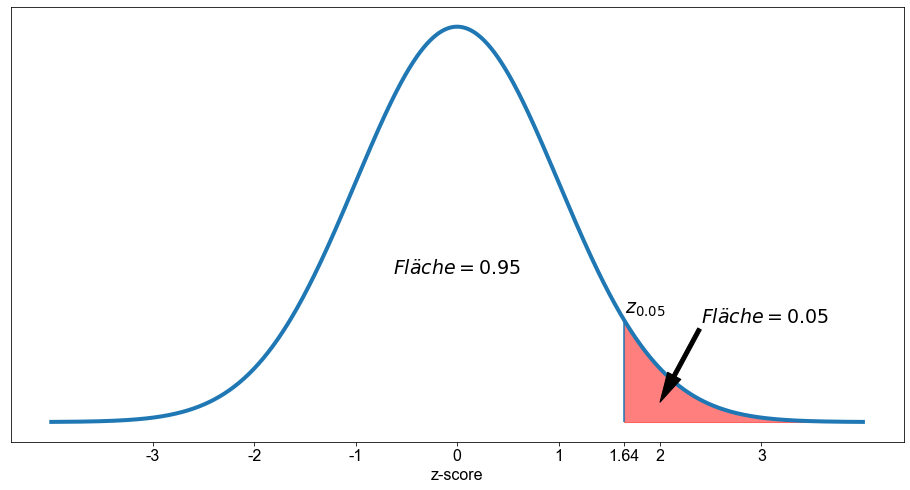
Um den entsprechenden \(z\)-Score zu erhalten, kann man ihn in einer Wahrscheinlichkeitstabelle nachschlagen oder Python verwenden. Daher wenden wir die Funktion norm.ppf an. Die norm.ppf-Funktion wird geschrieben als norm.ppf(p, mean = 0, scale = 1, loc = 0). Wir behalten die Standardwerte für die Argumente mean, sd und loc bei. Allerdings müssen wir vorsichtig sein auf welchen Bereich der Fläche unter der Normalverteilung wir uns beziehen. Für norm.ppf(p) erhalten wir den \(z\)-Score, bei dem das p-Argument der Bereich links von \(z\) ist. Wenn wir dagegen norm.ppf(1-p) berechnen, erhalten wir den \(z\)-Score, bei dem das p-Argument der Bereich rechts von \(z\) ist. Wenden wir uns an Python um dies zu verdeutlichen.
norm.ppf(0.05)
-1.6448536269514729
norm.ppf(0.95)
1.6448536269514722
Es ist interessant zu erwähnen das die Perzentile Punkt Funktion norm.ppf die inverse Funktion der kumulativen Wahrscheinlichkeitsfunktion norm.cdf ist
norm.cdf(norm.ppf(0.95))
0.95
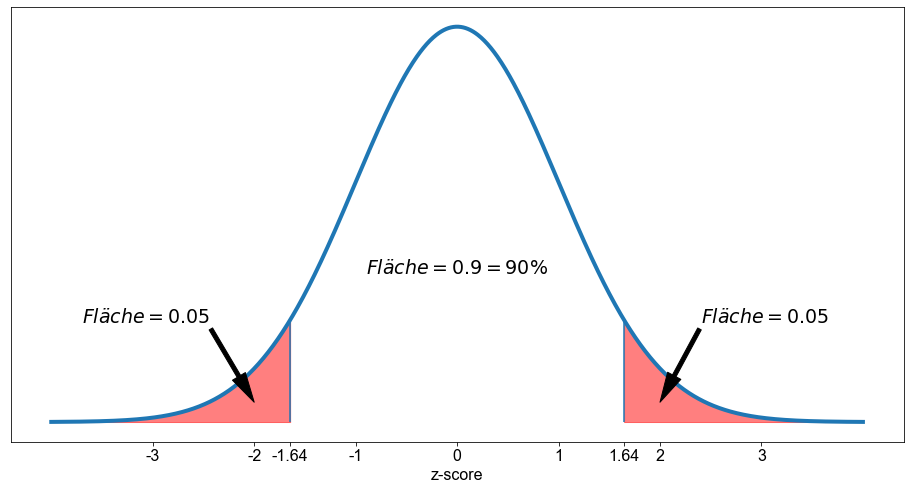
Da die Standardnormalverteilung symmetrisch ist, erhalten wir zweimal die gleiche Zahl, aber mit einem anderen Vorzeichen. Das bedeutet, dass bei einem z-Wert von etwa \(1,64 \ \) \( 95 \%\) aller Werte links von \(z_{0,05}\) und \(5 \%\) aller Werte rechts davon liegen. Im Gegensatz dazu liegen für einen \(z\)-Wert von etwa \(-1,64 \ \) \(5 \%\) aller Werte links von \(z_{0,05}\) und \(95 \%\) aller Werte rechts davon. Kombiniert man diese, erhält man das Intervall \(z \in [-1,64 \ \),\( \ 1,64 ]\), das \(90 \%\) aller Werte abdeckt.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 8))
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax.plot(x, norm.pdf(x), color="C0", linewidth=4)
z1 = norm.ppf(0.05)
z2 = norm.ppf(0.95)
for _x in [norm.ppf(0.05), norm.ppf(0.95)]:
ax.vlines(_x, ymin=-0, ymax=norm.pdf(_x, mu, sigma))
ticks = [-3, -2, z1, -1, 0, 1, z2, 2, 3]
ax.set_xticks(ticks)
ax.set_xticklabels([np.round(x, 2) if (x == z1) or (x == z2) else x for x in ticks])
ax.fill_between(x, norm.pdf(x), where=(x >= norm.ppf(0.95)), color="r", alpha=0.5)
ax.fill_between(x, norm.pdf(x), where=(x <= norm.ppf(0.05)), color="r", alpha=0.5)
ax.text(
0,
0.15,
s=r"$Fläche = 0.9 = 90\%$",
horizontalalignment="center",
size=19,
)
ax.annotate(
r"$Fläche=0.05$",
xy=(2, 0.02),
xytext=(2.4, 0.1),
# textcoords="data",
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=19,
)
ax.annotate(
r"$Fläche=0.05$",
xy=(-2, 0.02),
xytext=(-3.7, 0.1),
# textcoords="data",
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=19,
)
ax.set_xlabel(r"z-score")
ax.set_yticks([])
[]
Standardisierung einer normalverteilten Variable¶
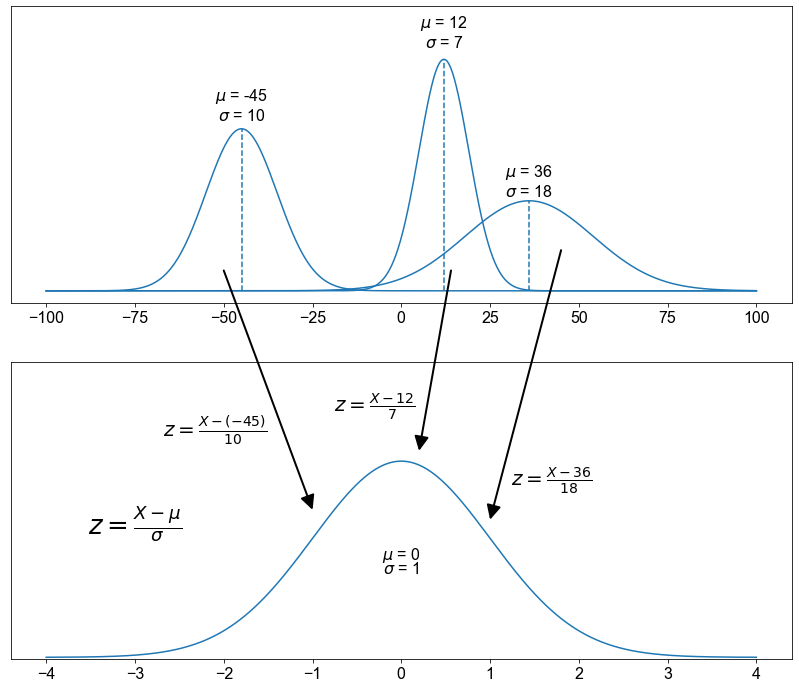
Bevor wir das Konzept der Standardnormalverteilung auf einen realen Datensatz anwenden können, müssen wir das Konzept der Standardisierung einer Normalverteilung diskutieren. Wir wissen, dass eine Normalverteilung durch zwei Parameter parametrisiert ist, ihren Mittelwert \(\sigma \in \mathbb R>0\) und ihre Standardabweichung \(\sigma \in \mathbb R>0,X \sim N(\mu,\sigma)\). Der tatsächliche Wert dieser Parameter hängt von der Population und den zur Beschreibung ihrer Merkmale verwendeten Metriken ab. Um ein bestimmtes \(\mu\) und \(\sigma\), das sich auf eine bestimmte Zufallsvariable X bezieht, in \(\mu=0\) und \(\sigma=1\) umzuwandeln, müssen wir den \(x\)-Wert in einen \(z\)-Wert umwandeln, indem wir die folgende Gleichung anwenden.
Als Ergebnis erhalten wir eine Standardnormalverteilung für eine bestimmte Normalverteilung. Dieses Verfahren ist unerlässlich, wenn Sie die \(z\)-Scores oder eine auf einen \(z\)-Score bezogene Wahrscheinlichkeit \((P(z))\) bestimmen müssen indem man sie in einer Tabelle nachschlägt. Wir werden später sehen, dass Python ein so mächtiges Werkzeug ist, dass der Schritt der Standardisierung überflüssig ist.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(14, 12), nrows=2)
# axis 0
x = np.linspace(-100, 100, 1000)
mu = -45
sigma = 10
ax[0].plot(x, norm.pdf(x, mu, sigma), color="C0")
ax[0].vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax[0].text(
mu,
norm.pdf(mu, mu, sigma) * 1.05 + 0.005,
s=f"$\mu$ = {mu}",
horizontalalignment="center",
size=16,
)
ax[0].text(
mu,
norm.pdf(mu, mu, sigma) * 1.05,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=16,
)
mu = 12
sigma = 7
ax[0].plot(x, norm.pdf(x, mu, sigma), color="C0")
ax[0].vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax[0].text(
mu,
norm.pdf(mu, mu, sigma) * 1.05 + 0.005,
s=f"$\mu$ = {mu}",
horizontalalignment="center",
size=16,
)
ax[0].text(
mu,
norm.pdf(mu, mu, sigma) * 1.05,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=16,
)
mu = 36
sigma = 18
ax[0].plot(x, norm.pdf(x, mu, sigma), color="C0")
ax[0].vlines(mu, ymin=0, ymax=norm.pdf(mu, mu, sigma), linestyle="dashed")
ax[0].text(
mu,
norm.pdf(mu, mu, sigma) * 1.05 + 0.005,
s=f"$\mu$ = {mu}",
horizontalalignment="center",
size=16,
)
ax[0].text(
mu,
norm.pdf(mu, mu, sigma) * 1.05,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=16,
)
ax[0].set_ylim(-0.003, 0.07)
# axis 1
x = np.linspace(-4, 4, 1000)
mu = 0
sigma = 1
ax[1].plot(x, norm.pdf(x), color="C0")
ax[1].text(
0,
0.2,
s=f"$\mu$ = {mu}",
horizontalalignment="center",
size=16,
)
ax[1].text(
0,
0.17,
s=f"$\sigma$ = {sigma}",
horizontalalignment="center",
size=16,
)
ax[1].text(
-3,
0.25,
s=r"$z = \frac{X-\mu}{\sigma}$",
horizontalalignment="center",
size=26,
)
ax[1].text(
-2.1,
0.45,
s=r"$z = \frac{X-(-45)}{10}$",
horizontalalignment="center",
size=20,
)
ax[1].text(
-0.3,
0.5,
s=r"$z = \frac{X-12}{7}$",
horizontalalignment="center",
size=20,
)
ax[1].text(
1.7,
0.35,
s=r"$z = \frac{X-36}{18}$",
horizontalalignment="center",
size=20,
)
# Add line from one subplot to the other
from matplotlib.patches import ConnectionPatch
for xy in [
([45, 0.01], [1, 0.28]),
([14, 0.005], [0.2, 0.42]),
([-50, 0.005], [-1, 0.3]),
]:
xyA = xy[0]
xyB = xy[1]
# ConnectionPatch handles the transform internally so no need to get fig.transFigure
arrow = ConnectionPatch(
xyA,
xyB,
coordsA=ax[0].transData,
coordsB=ax[1].transData,
# Default shrink parameter is 0 so can be omitted
color="black",
arrowstyle="-|>", # "normal" arrow
mutation_scale=30, # controls arrow head size
linewidth=2,
)
fig.patches.append(arrow)
ax[1].set_ylim(-0.003, 0.6)
for _ax in ax:
_ax.set_yticks([])
Die Standard-Normalverteilung: Ein Beispiel in Python¶
Vorbereitung der Daten¶
Jetzt sind wir bereit, einige Übungen zu machen. Dazu laden wir den students Datensatz. Sie können die Datei students.csv hier herunterladen. Zuerst laden wir den Datensatz und geben ihm einen passenden Namen.
# Lese Datei students.csv als Dataframe ein
students = pd.read_csv("../../data/students.csv")
# Lese Spalte 'height' ein
height = students["height"]
Der students Datensatz besteht aus \(8239\) Zeilen, von denen jede einen bestimmten Studenten repräsentiert, und \(16\) Spalten, von denen jede einer Variable/einem Merkmal entspricht, das sich auf diesen bestimmten Studenten bezieht. Diese selbsterklärenden Variablen sind: stud_id, Name, Geschlecht, Alter, Größe, Gewicht, Religion, nc_score, Semester, Hauptfach, Nebenfach, score1, score2, online_tutorial, graduated, salary. In diesem Abschnitt verwenden wir die Variable height, um das bisher Besprochene zu üben.
Zunächst wollen wir sicherstellen, dass wir es mit normalverteilten Daten zu tun haben. Wenn eine Variable normalverteilt ist, sollte ein Histogramm der Beobachtungen bei einer großen Stichprobe in etwa die Form einer Glocke haben.
# Plotte die Werte als Histogramm
fig, ax = plt.subplots()
ax.hist(height, bins=14, edgecolor="k")
# Erzeuge Labels
ax.set_ylabel("Häufigkeit")
ax.set_xlabel("Größe in cm")
Text(0.5, 0, 'Größe in cm')
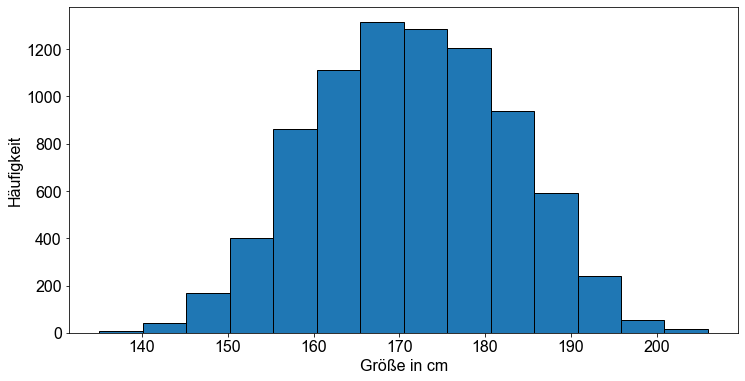
Aus dem Diagramm kann man schließen, dass die Variable height normalverteilt ist. Allerdings ist es vor allem bei kleinen Stichproben oft schwierig, eine klare Form in einem Histogramm festzustellen, insbesondere, ob sie glockenförmig ist. Daher ist eine empfindlichere grafische Technik zur Beurteilung der Normalität erforderlich. Normal-Quantil-Plot bieten eine solche Technik. Die Idee hinter einem Normal-Quantil-Plot oder kurz Q-Q Plot ist einfach: Man vergleicht die beobachteten Werte der Variablen mit den Beobachtungen, die für eine normalverteilte Variable erwartet werden. Genauer gesagt ist ein Q-Q Plot eine Darstellung der beobachteten Werte der Variablen im Vergleich zu den Werten, die für eine Variable mit der Standardnormalverteilung erwartet werden. Wenn die Variable normalverteilt ist, sollte der Q-Q Plot in etwa linear sein (d. h. in etwa auf einer Geraden liegen) (Fahrmeir et al. [2016] s.88).
Bei der Verwendung eines Normal-Quantil-Plots zur Beurteilung der Normalität einer Variablen sind zwei Dinge zu beachten:
Die Entscheidung, ob eine normale Wahrscheinlichkeitsverteilung annähernd linear ist, ist eine subjektive Entscheidung, und
dass wir nur eine begrenzte Anzahl von Beobachtungen dieser bestimmten Variablen verwenden, um ein Urteil über alle möglichen Beobachtungen der Variablen zu fällen.
In Python können wir die Funktion qqplot() verwenden, um Normalwahrscheinlichkeitsplots zu erstellen, die auch als Q-Q-Plots bezeichnet werden.
# Erzeuge Q-Q Plot
_ = smi.qqplot(height, line="r")

Bei der Betrachtung des Diagramms sehen wir, dass die Quantile der Stichprobe im Vergleich zu den theoretischen Quantilen am unteren und oberen Ende etwas abweichen. Dieser Tatsache muss etwas mehr Aufmerksamkeit geschenkt werden! Was könnte der Grund für die Abweichung am oberen und unteren Ende der Verteilung sein? Irgendeine Vermutung?
Was ist mit dem Geschlecht? Ehrlich gesagt scheint es natürlich zu sein, dass die durchschnittliche Körpergröße von Männern und Frauen unterschiedlich ist. Stellen wir ein Histogramm der Körpergröße von Männern und Frauen auf.
male_height = students.loc[students["gender"] == "Male", "height"]
female_height = students.loc[students["gender"] == "Female", "height"]
# Plotte die Werte als Histogramm
fig, ax = plt.subplots()
# Bestimme Anzahl Bins
bins_male = male_height.max() - male_height.min()
ax.hist(male_height, bins_male, edgecolor="k", alpha=0.5)
# Bestimme Anzahl Bins
bins_female = female_height.max() - female_height.min()
ax.hist(female_height, bins_female, edgecolor="r", alpha=0.5)
# Erzeuge Labels
ax.set_ylabel("Häufigkeit")
ax.set_xlabel("Größe in cm")
Text(0.5, 0, 'Größe in cm')
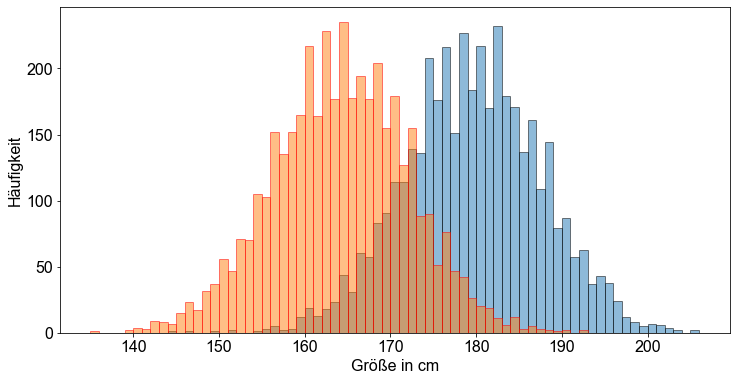
Das ist es! Offensichtlich haben die beiden Gruppen unterschiedliche Mittelwerte, so dass die Zusammenfassung zu einer Gruppe dazu führt, dass die linken und rechten Ausläufer der sich ergebenden Verteilung weiter reichen, als bei einer normalverteilten Variablen zu erwarten wäre. Um fortzufahren, betrachten wir also nur die Körpergröße der Studentinnen. Der Klarheit halber zeichnen wir noch einmal den Normalwahrscheinlichkeitsplit der Größenvariablen, um sicherzustellen, dass unsere Zielvariablen normalverteilt sind.
# Erzeuge Q-Q Plot
_ = smi.qqplot(female_height, line="r")
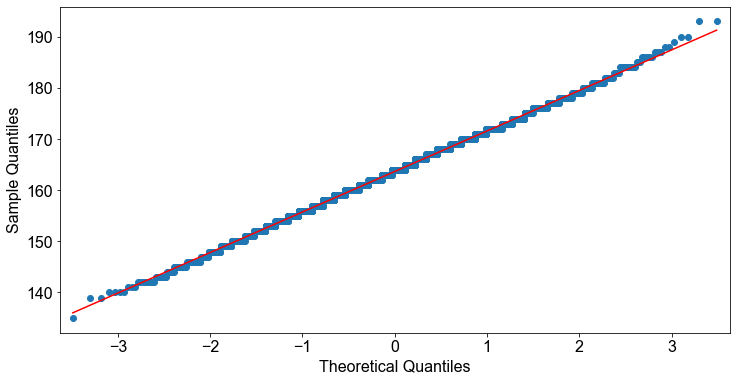
Bevor wir mit den eigentlichen Übungen beginnen, berechnen wir zunächst den Mittelwert \(\bar{x}\) und die Standardabweichung \(s\) der Zielvariablen. Außerdem standardisieren wir die Variable, um eine Standardnormalverteilung mit \(\bar{x}=0\) und \(s=1\) zu erhalten, und weisen ihr einen geeigneten Variablennamen zu.
# Heights
height_mean = female_height.mean()
height_mean
163.65328467153284
height_sd = female_height.std()
height_sd
7.919725792052593
height_z = (female_height - height_mean) / height_sd
Die Variable height hat einen Mittelwert von \(163,7\) cm und eine Standardabweichung von \(7,9\) cm.
Suche nach dem Bereich links von einem angegebenen \(z\)-Scores oder \(x\)-Wertes¶
Frage 1
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Studentin aus dem students Datensatz eine Körpergröße von \(168\) cm oder weniger hat? Wir suchen also nach \(P(x \le 168)\).
Zunächst berechnen wir die Wahrscheinlichkeit für die standardisierte Variable. Dazu müssen wir den Wert, der uns interessiert (\(168\) cm), in einen \(z\)-Score umwandeln.
height_z2 = (168 - height_mean) / height_sd
height_z2
0.5488466952768823
Dann müssen wir die Fläche unter der Kurve links neben dem erhaltenen \(z\)-Wert berechnen. Zur Erinnerung: Die Fläche unter der Kurve einer normalverteilten Variablen kann mit Hilfe der Funktion norm.cdf() berechnet werden. Die norm.cdf() -Funktion wird als norm.cdf(q, loc = 0, scale = 1) geschrieben. Für dieses spezielle Beispiel können wir alle Standardargumente akzeptieren.
norm.cdf(height_z2)
0.7084446690628331
Genial, wir haben ein Ergebnis: \(P(z\le 0,55) \approx 0,71\)
Nun führen wir die gleiche Berechnung durch, überspringen aber diesmal den Schritt der Standardisierung. Dank der Leistungsfähigkeit von Python müssen wir uns nicht auf Tabellen verlassen, sondern können den Stichprobenmittelwert \(\bar x\) und die Standardabweichung der Stichprobe, \(s\), in die Funktion stats.norm.cdf eingeben.
x = 168
norm.cdf(x, loc=height_mean, scale=height_sd)
0.7084446690628331
Perfekt! Die Zahlen stimmen überein: \(P(x \le 168) \approx 0,71\). Um sicherzustellen, dass wir verstehen, was vor sich geht, werden unten sowohl die Fläche unter der Kurve für die standardisierte Variable in \(z\)-Werten (linkes Feld) als auch die Fläche für die nicht standardisierte Variable in cm (rechtes Feld) dargestellt.
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(16, 6), ncols=2)
# axis 0
x = np.linspace(-3.2, 3.2, 1000)
mu = 0
sigma = 1
ax[0].plot(x, norm.pdf(x), color="C0", linewidth=4)
z = 0.55
ticks = [-3, -2, -1, 0, z, 1, 2, 3]
ax[0].vlines(z, ymin=0, ymax=norm.pdf(z, mu, sigma))
ax[0].set_xticks(ticks)
ax[0].set_xticklabels([np.round(x, 2) if x == z else str(x) for x in ticks])
ax[0].fill_between(x, norm.pdf(x), where=x <= z, color="r", alpha=0.5)
ax[0].annotate(
r"$Fläche \approx 0.71$",
xy=(-0.2, 0.25),
xytext=(-3.45, 0.3),
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=19,
)
ax[0].set_title(r"$P(z \leq 0.55)$", size=18)
# axis 1
x = np.linspace(height_mean + height_sd * -3.2, height_mean + height_sd * 3.2, 1000)
mu = height_mean
sigma = height_sd
ax[1].plot(x, norm.pdf(x, mu, sigma), color="C0", linewidth=4)
z = 168
ax[1].vlines(z, ymin=0, ymax=norm.pdf(z, mu, sigma))
ticks = ax[1].get_xticks().tolist()
ticks.pop(ticks.index(170))
ticks = ticks + [z]
ax[1].set_xticks(ticks)
ax[1].fill_between(x, norm.pdf(x, mu, sigma), where=x <= z, color="r", alpha=0.5)
ax[1].annotate(
r"$Fläche \approx 0.71$",
xy=(163, 0.03),
xytext=(137, 0.04),
arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
size=19,
)
ax[1].set_title(r"$P(z \leq 168)$", size=18)
for _ax in ax:
_ax.set_yticks([])
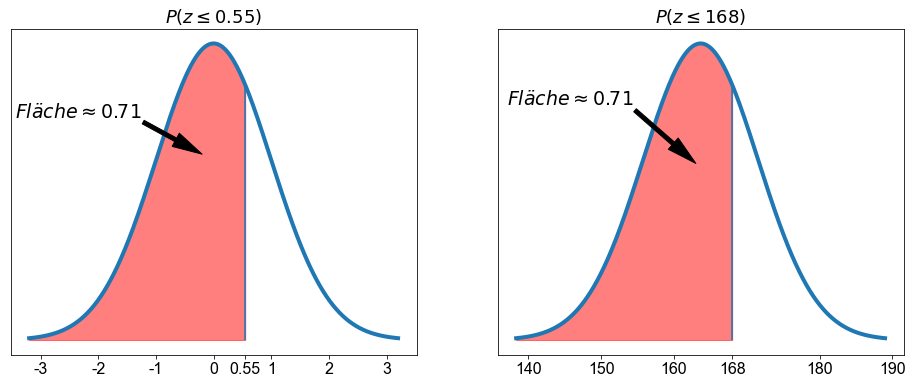
Ermitteln der Fläche rechts von einem bestimmten \(x\)-Wert¶
Frage 2
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Studentin aus dem students Datensatz eine Körpergröße von \(185\) cm oder mehr hat? Wir suchen also nach \(P(x \ge 175)\). Um die Fläche unter der Kurve rechts vom interessierenden Wert zu erhalten, müssen wir in die Funktion stats.norm.sf() oder 1-stats.norm.cdf verwenden.
x = 175 # height in cm
norm.sf(x, loc=height_mean, scale=height_sd)
0.07596955321865
x = 175 # height in cm
norm.cdf(x, loc=height_mean, scale=height_sd)
0.92403044678135
Antwort: : \(P(x \ge 175) \approx 0,08\)
Ermitteln der Fläche zwischen zwei angegebenen \(x\)-Werten¶
Um die Fläche unter einer Kurve für ein Intervall \([a \ \),\( \ b]\) zu bestimmen, verwenden wir die Gleichung
Frage 3
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Studentin aus dem students Datensatz eine Körpergröße zwischen \(155\) und \(165\) cm hat, \(P(155≤x≤165)\)?
x_lower = 155 # height in cm
x_upper = 165 # height in cm
cdf_upper = norm.cdf(x_upper, loc=height_mean, scale=height_sd)
cdf_lower = norm.cdf(x_lower, loc=height_mean, scale=height_sd)
cdf_upper - cdf_lower
0.4302335028797312
Antwort: : \(P(155≤x≤165)≈0,43\)
Frage 4
Wie hoch ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Studentin aus dem Studentendatensatz eine Körpergröße zwischen \(170\) und \(180\) cm hat, \(P(170≤x≤180)\)?
x_lower = 170 # height in cm
x_upper = 180 # height in cm
cdf_upper = norm.cdf(x_upper, loc=height_mean, scale=height_sd)
cdf_lower = norm.cdf(x_lower, loc=height_mean, scale=height_sd)
cdf_upper - cdf_lower
0.19194918877717126
Antwort: : \(P(170≤x≤180)≈0,19\)
\(z_\alpha\) finden¶
Frage 5
Wir möchten wissen, welche Körpergröße der Studentinnen in unserem students Datensatz mit einer Wahrscheinlichkeit von \(0,60\) übereinstimmt. Oder anders ausgedrückt: Wenn wir eine Anzahl von \(n\) Studenten aus dem students Datensatz zufällig auswählen, welche Größe teilt die Stichprobe in \(60 \%\) der \(n\) Studierenden, die kleiner sind, und \(40 \%\) der n Studentinnen, die größer als diese bestimmte Größe sind. Wir suchen also nach \(P(X<?)=0,60\).
Um \(P(X<?)=0,60\) zu lösen, werden wir zwei Ansätze wählen. Der erste Ansatz verwendet den \(z\)-Score, und der zweite verwendet Python, um den Standardisierungsschritt überflüssig zu machen. .
Für beide Ansätze verwenden wir die norm.ppf()-Funktion, die wie folgt geschrieben wird: norm.ppf(p, loc = 0, scale = 1).
Für den ersten Ansatz müssen wir die Gleichung für die Standardisierung von oben umstellen und sie für \(x\) lösen
Für die Berechnung von \(x\) benötigen wir den Mittelwert (height_mean) und die Standardabweichung (height_sd) für die Variable height, die \(163,7\) cm bzw. \(7,9\) cm beträgt. Außerdem müssen wir einen \(z\)-Score für die gegebene Wahrscheinlichkeit von \(0,60\) erhalten. Wir können diesen \(z\)-Score in einer Tabelle nachschlagen oder die norm.ppf()-Funktion in Python anwenden. Wir wollen den \(z\)-Score ermitteln, bei dem der Bereich links von diesem \(z\)-Score \(0,60\) entspricht; erinnern Sie sich, dass wir nach \(P(X<?)=0,60\) suchen.
z = norm.ppf(0.6, loc=0, scale=1)
z
0.2533471031357997
Da wir nun \(z\) kennen, können wir in die Gleichung von oben einsetzen
\( x = z \sigma + \mu \)
\( = 0,25 \times 7,9 + 163,7 \)
\( \approx 165,66 \)
Perfekt, wir sind fertig: \(P(X<165,66)=0,60\)
Nun gehen wir den zweiten Ansatz durch, bei dem wir den Schritt der \(z\)-Berechnung überspringen. Alles, was wir tun müssen, ist, die norm.ppf()-Funktion mit dem Mittelwert und der Standardabweichung unserer Variablen height zu füttern.
x = norm.ppf(0.6, loc=height_mean, scale=height_sd)
x
165.65972425857925
Keine Überraschung, die Zahlen stimmen überein: \(P(X<165,66)=0,60\).
