Die Chi-Quadrat-Verteilung
Contents
Die Chi-Quadrat-Verteilung¶
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import chi2
Die Chi-Quadrat (\(\chi^2\)) ist eine der wichtigsten kontinuierlichen Wahrscheinlichkeitsverteilungen mit vielen Anwendungen in der statistischen Theorie und Inferenz ([Papula, 2016] s.441).
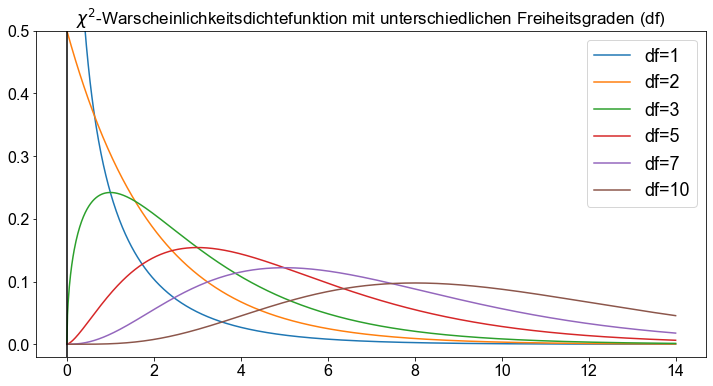
Sei \(n \gt 0\) eine positive ganze Zahl. Für eine Zufallsvariable, die eine (\(\chi^2\))-Verteilung mit \(n\) Freiheitsgraden (\(df\)) hat, lautet die Wahrscheinlichkeitsdichtefunktion
wobei \(\Gamma\) die Gamma-Funktion bezeichnet. Die (\(\chi^2\))-Verteilung (mit \(n\) Freiheitsgraden) ist gleich der \(\Gamma\)-Verteilung mit den Parametern \((n/2,2)\), d. h. mit Mittelwert und Varianz gleich \(n\) bzw. \(2n\).
from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt
df = [1, 2, 3, 5, 7, 10]
x = np.linspace(0, 14, 1000)
fig, ax = plt.subplots()
for _df in df:
ax.plot(x, chi2.pdf(x, df=_df), label=f"df={_df}")
ax.set_title(
"$\chi^2$-Warscheinlichkeitsdichtefunktion mit unterschiedlichen Freiheitsgraden (df)"
)
ax.legend(fontsize=18)
ax.set_ylim(-0.02, 0.5)
ax.axvline(0, color="k")
<matplotlib.lines.Line2D at 0x16cfd0520>
Grundlegende Eigenschaften von \(\chi^2\)-Kurven
Die Gesamtfläche unter einer \(\chi^2\)
Kurve ist gleich \(1\)
Eine \(\chi^2\)-Kurve beginnt bei \(0\) auf der horizontalen Achse und erstreckt sich unendlich weit nach rechts, wobei sie sich der horizontalen Achse nähert, diese aber nie berührt.
Eine \(\chi^2\)-Kurve ist rechtsschief.
Mit zunehmender Anzahl von Freiheitsgraden sehen \(\chi^2\)-Kurven zunehmend wie normalverteilt aus.
Die Chi-Quadrat-Verteilung in Python¶
Die wichtigsten Funktionen zur Interaktion mit der \(\chi^2\)-Verteilung sind chi2.pdf(), chi2.cdf(), chi2.ppf(), chi2.rvs(). Die Funktion chi2.pdf() liefert die Dichte, die Funktion chi2.cdf() die Verteilungsfunktion, die Funktion chi2.ppf() die Quantilfunktion und die Funktion chi2.rvs() die Zufallsabweichungen.
Wir verwenden die Funktion chi2.pdf(), um die Dichte für die ganzzahligen Werte \(4\) bis \(8\) einer \(\chi^2\)-Kurve mit \(df=7\).
for i in range(4, 9):
print(chi2.pdf(i, df=7))
0.11518072856146785
0.12204152134938738
0.11676521599113948
0.10411977480817192
0.08817913751079275
Wir verwenden chi2.cdf(), um die Fläche unter der Kurve für das Intervall \([0,6]\) und das Intervall \([6,\infty[\) einer\(\chi^2\)-Kurve mit \(df=7\) zu berechnen. Weiter fragen wir Python, ob die Summe der Intervalle \([0,6]\) und \([6,\infty[\) den Wert \(1\) ergibt.
chi2_cdf1 = chi2.cdf(6, df=7)
chi2_cdf1
0.4602506496044429
chi2_cdf2 = 1 - chi2.cdf(6, df=7)
chi2_cdf2
0.539749350395557
chi2_cdf1 + chi2_cdf2
1.0
Wir verwenden chi2.ppf(), um das Quantil für eine bestimmte Fläche (= Wahrscheinlichkeit) unter der Kurve für eine \(\chi^2\)-Kurve mit \(df=7\) zu berechnen, die \(q=0,25\),\(0,5\),\(0,75\) und \(0,999\) entspricht.
chi2.ppf(0.25, df=7)
4.2548521835465145
chi2.ppf(0.5, df=7)
6.345811195521515
chi2.ppf(0.75, df=7)
9.037147547908143
chi2.ppf(0.999, df=7)
24.321886347856854
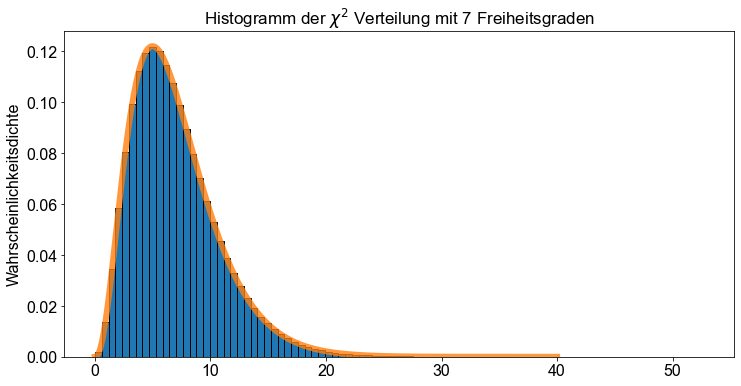
Wir verwenden die Funktion chi2.rvs(), um \(100.000\) Zufallswerte aus der\(\chi^2\)-Verteilung mit \(df=7\) zu erzeugen. Anschließend zeichnen wir ein Histogramm und vergleichen es mit der Wahrscheinlichkeitsdichtefunktion der \(\chi^2\)-Verteilung mit \(df=7\) (orangefarbene Linie).
# Erzeuge Chi^2 Werte
chi2_rvs = chi2.rvs(df=7, size=10000000)
# Erzeuge x-werte
x = np.linspace(0, 40, num=1000)
# Plotte chi2-Verteilung
fig, ax = plt.subplots()
ax.set_title("Histogramm der $\chi^2$ Verteilung mit 7 Freiheitsgraden")
ax.set_ylabel("Wahrscheinlichkeitsdichte")
ax.hist(chi2_rvs, bins=90, edgecolor="k", density=True)
ax.plot(x, chi2.pdf(x, df=7), linewidth=6, alpha=0.8)
[<matplotlib.lines.Line2D at 0x16d789a80>]