Die Binomialverteilung
Contents
Die Binomialverteilung¶
import math
import random
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom
Viele Anwendungen der Wahrscheinlichkeitsrechnung und Statistik betreffen die Wiederholung eines Experiments. Wir nennen jede Wiederholung einen Versuch, und wir sind besonders an Fällen interessiert, in denen das Experiment (jeder Versuch) nur zwei mögliche Ergebnisse hat: Erfolg oder Misserfolg, wahr oder falsch, \(0\) oder \(1\).
Um wiederholte Versuche eines Experiments mit zwei möglichen Ergebnissen zu analysieren, benötigen wir Kenntnisse über Fakultäten, Binomialkoeffizienten und Bernoulli-Versuche.
Auf der Grundlage dieser Voraussetzungen lernen wir die Binomialverteilung kennen, die eine Wahrscheinlichkeitsverteilung für die Anzahl der Erfolge in einer Folge von Bernoulli-Versuchen ist ([Fahrmeir et al., 2016] s.213,s.289).
Voraussetzungen¶
Fakultät¶
Das Produkt der ersten \(k\) positiven ganzen Zahlen wird als \(k\)-Faktultät bezeichnet und mit \(k!\) abgekürzt ([Fahrmeir et al., 2016] s.186).
Wir definieren auch \(0!=1\).
Betrachten wir ein einfaches Beispiel und berechnen die Fakultät von \(6\). Wenn wir die obige Gleichung einsetzen, erhalten wir folgendes Ergebnis
In Python können wir das entweder direkt berechnen…
6 * 5 * 4 * 3 * 2 * 1
720
…oder wir verwenden die eingebaute Funktion factorial()
math.factorial(6)
720
Binomialkoeffizienten¶
Wenn \(n\) eine positive ganze Zahl und \(k\) eine nicht negative ganze Zahl kleiner oder gleich \(n\) ist, dann ist der Binomialkoeffizient \({n \choose k}\) definiert als:
Die Binomialkoeffizienten \({n \choose k}\) werden oft als “\(n\) über \(k\)” gelesen, weil es \({n \choose k}\) Möglichkeiten gibt, \(k\) Elemente ohne Rücksicht auf ihre Reihenfolge aus einer Menge von \(n\) Elementen auszuwählen. Mit anderen Worten: Die Binomialkoeffizienten beziehen sich auf die Anzahl der Kombinationen von \(n\) Dingen, die \(k\)-mal ohne Wiederholung ausgewählt werden. Bitte beachten Sie, dass die Reihenfolge der Auswahl keine Rolle spielt.
Versuchen wir es mit einem Beispiel, um ein Gefühl dafür zu bekommen.
Nehmen wir ein einfaches Wort wie “dog”, das drei verschiedene Buchstaben enthält: d, o, g. Wie viele Möglichkeiten gibt es, genau einen Buchstaben aus diesen \(3\) Buchstaben zu ziehen? Mit Sicherheit gibt es \(3\) Möglichkeiten, genau einen Buchstaben zu zeichnen: “d”, “o”, oder “g”. Wir können also alle Kombinationen als \({3 \choose 1}\) schreiben. Was ist mit zwei Buchstaben? Wie viele Kombinationen gibt es, um genau zwei Buchstaben aus \(3\) Buchstaben zu ziehen? Die Kombinationen sind “do”, “dg” und “og” (Bitte beachten Sie, dass z.B. “og” und “go” nur als eine Kombination gezählt werden, da die Reihenfolge im Moment keine Rolle spielt). Dementsprechend ist die Antwort \(3\), die als \({3 \choose 2}\) geschrieben werden kann. Eine letzte Frage: Wie viele Kombinationen gibt es, um aus \(3\) Buchstaben genau drei Buchstaben zu ziehen? Fragen wir Python!
Zunächst wenden wir einen naiven Ansatz an, indem wir die obige Formel anwenden.
# n entspricht 3 Buchstaben von dog
n = 3
# k entspricht wir ziehen 3 Buchstaben
k = 3
math.factorial(n) / ((math.factorial(k) * math.factorial(n - k)))
1.0
Wir können aber auch die eingebaute Funktion math.comb() verwenden, um die Anzahl der Kombinationen zu berechnen. Wir machen das für \(k=1,2,3\).
# 3 über 1
math.comb(3, 1)
3
# 3 über 2
math.comb(3, 2)
3
# 3 über 3
math.comb(3, 3)
1
Nun, da wir mit dem Konzept vertraut sind, wollen wir ein komplexeres Beispiel betrachten: Die SRH Hochschule bittet alle Absolventen, ihre \(4\) Lieblingskurse aus dem Studienplan zu wählen. Wie viele verschiedene Antworten könnten die Studierenden geben, wenn der Studienplan \(24\) Kurse zur Auswahl anbietet? Irgendwelche Vermutungen? Lassen Sie uns Python fragen!
math.comb(24, 4)
10626
Die Studenten können \(10.626\) verschiedene Antworten geben.
Bernoulli-Versuche¶
Wiederholte Versuche eines Experiments werden als Bernoulli-Versuche bezeichnet, wenn die folgenden drei Bedingungen erfüllt sind:
Das Experiment (jeder Versuch) hat zwei mögliche Ergebnisse, die mit \(s\) für Erfolg und \(f\) für Misserfolg bezeichnet werden.
Die Versuche sind unabhängig voneinander.
Die Wahrscheinlichkeit für einen Erfolg, die als Erfolgswahrscheinlichkeit bezeichnet wird und mit \(p\) bezeichnet wird, bleibt von Versuch zu Versuch gleich.
Die Binomialverteilung¶
Die Binomialverteilung ist die Wahrscheinlichkeitsverteilung für die Anzahl der Erfolge in einer Folge von Bernoulli-Versuchen ([Papula, 2016] s.350).
Die binomische Wahrscheinlichkeitsformel¶
Bei \(n\) Bernoulli-Versuchen ist die Anzahl der Ergebnisse, die genau \(x\) Erfolge enthalten, gleich dem Binomialkoeffizienten \({n \choose x}\) ([Fahrmeir et al., 2016] s.188).
\(X\) sei die Gesamtzahl der Erfolge in \(n\) Bernoulli-Versuchen mit der Erfolgswahrscheinlichkeit \(p\). Dann ist die Wahrscheinlichkeitsverteilung der Zufallsvariablen \(X\) gegeben durch:
Die Zufallsvariable \(X\) wird als Binomialzufallsvariable bezeichnet und folgt der Binomialverteilung mit den Parametern \(n\) und \(p\) ([Papula, 2016] s.356).
Betrachten wir ein Beispiel aus der realen Welt.
Langzeitstatistiken besagen, dass die Chance, die Abschlussprüfung in Statistik zu bestehen, bei \(0,3\) liegt. Ja, etwa \(70 \%\) der Studenten fallen in der Statistikprüfung durch! Übrigens, wenn Sie dieses E-Learning-Modul absolvieren, werden Ihre Chancen, die Abschlussprüfung zu bestehen, definitiv steigen :-)
Betrachten wir eine Klasse mit \(25\) Studenten. Wie hoch ist die Wahrscheinlichkeit, dass genau \(3\) der Studenten dieser Klasse die Abschlussprüfung in Statistik bestehen werden? Oder anders ausgedrückt: \(P(X=3)\). Auch hier beginnen wir mit der Implementierung eines naiven Ansatzes in Python.
# Anzahl der Studenten
n = 25
# Erfolgswahrscheinlichkeit
p = 0.3
# Anzahl der Studenten die die Prüfung bestehen
k = 3
math.comb(n, k) * p ** (k) * (1 - p) ** (n - k)
0.02427998871170032
Wow, die Wahrscheinlichkeit, dass genau \(3\) von \(25\) Studierenden \((P(X=3))\) die Abschlussprüfung in Statistik bestehen, ist ziemlich gering. Wie sieht es mit der Wahrscheinlichkeit aus, dass genau \(15\) von \(25\) Studierenden \((P(X=15))\) die Abschlussprüfung in Statistik bestehen werden? Wir wenden uns an Python.
# Anzahl der Studenten
n = 25
# Erfolgswahrscheinlichkeit
p = 0.3
# Anzahl der Studenten die die Prüfung bestehen
k = 15
math.comb(n, k) * p ** (k) * (1 - p) ** (n - k)
0.0013248974242351928
Die Wahrscheinlichkeit von \(P(X=15)\) beträgt etwa \(0,1 \%\). Wir könnten mit unseren Experimenten fortfahren, um alle Wahrscheinlichkeiten für genau ein Ergebnis für \(k=0,1,2, \dots ,n\) herauszufinden. Bitte beachten Sie allerdings, dass es für unser spezielles Beispiel nicht sehr informativ ist, die Wahrscheinlichkeit für das Bestehen der Prüfung für genau eine bestimmte Anzahl \((k)\) von Studenten zu kennen. Für uns ist es von größerem Informationsinteresse, wenn wir die Frage beantworten könnten, wie hoch die Wahrscheinlichkeit ist, dass \(k\) oder weniger Studierende \((P(X \le k))\) die Prüfung bestehen, oder, was ebenso interessant ist, dass \(k\) oder mehr Studierende \((P(X \ge k))\) die Prüfung bestehen.
Als Übung wenden wir uns an Python und bestimmen die Wahrscheinlichkeit, dass \(9\) oder weniger Studierende die Abschlussprüfung in Statistik bestehen \((P(X \le 9))\). Wir interessieren uns also für die Wahrscheinlichkeit, dass \(0\) von \(25 \ \),\( \ 1\) von \(25 \ \),\( \ 2\) von \(25 \ \),\( \ ...\) oder \(9\) von \(25\) Studierenden die Prüfung bestehen. Um diese Wahrscheinlichkeit zu berechnen, können wir unseren naiven Ansatz erweitern und Folgendes berechnen
\(P(X = 0)+P(X = 1)+P(X = 2)+ \dots+P(X = 9)\)
# Anzahl der Studenten
n = 25
# Erfolgswahrscheinlichkeit
p = 0.3
# Anzahl der maximalen Erfolge
k = 9
prob = 0
prob_total = 0
# Erzeuge for-loop
for i in range(k + 1):
prob = math.comb(n, i) * p ** (i) * (1 - p) ** (n - i)
prob_total += prob
prob_total
0.8105639764950532
Die Wahrscheinlichkeit, dass \(9\) oder weniger Studierende die Statistikprüfung bestehen \((P(X≤9))\), beträgt \(81,1 \%\). Das wiederum bedeutet, dass die Wahrscheinlichkeit, dass \(10\) oder mehr Studierende die Prüfung bestehen, \(P(X>9)=1-P(X≤9)\) oder nur \(18,9 \%\) beträgt.
Neben der ehrlich gesagt recht unangenehmen Einsicht in die Statistik des Bestehens der Abschlussprüfung ist es klar, dass die naive Implementierung von oben ziemlich mühsam ist. Deshalb führen wir die eingebauten Funktionen binom.pmf() und binom.cdf() ein.
Die Verwendung von binom.pmf() ist wie folgt: binom.pmf(k, n, p, loc). Wir lassen vorerst das Argument loc außer Acht. Somit vereinfacht sich die Funktion binom.pmf() zu binom.pmf(k, n, p), wobei \(k\) den insgesamten Erfolgen, \(n\) der Gesamtanzahl und \(p\) der Wahrscheinlichkeit für das Bestehen der Prüfung entspricht. Um zu überprüfen, ob die Funktion binom.pmf() wie erwartet funktioniert, erinnern wir uns an unsere Testbeispiele von oben, nämlich \(P(X=3)\) und \(P(X=15)\).
binom.pmf(3, 25, 0.3)
0.024279988711700378
binom.pmf(15, 25, 0.3)
0.0013248974242351943
Vergleichen Sie diese Ergebnisse mit den Ergebnissen unserer naiven Implementierung (scrollen Sie nach oben). Die Zahlen sollten übereinstimmen.
Die Funktion binom.pmf() ist sehr praktisch, wenn wir Wahrscheinlichkeiten akkumulieren wollen, wie z. B. \(P(X≤x)\) oder \(P(X>x)\), denn wir können eine for - Schleife für das Argument \(x\) angeben und anschließend summieren. Betrachten wir das Beispiel von oben \((P(X≤9))\).
P_le9 = []
for i in range(10):
P_le9.append(binom.pmf(i, 25, 0.3))
P_le = sum(P_le9)
P_le
0.8105639764950541
Eine weitere eingebaute Funktion, die für die Beantwortung von \(P(X≤9)\) geeignet ist, ist die Funktion binom.pdf(), die die Verteilungsfunktion zurückgibt. Die Funktion binom.cdf() berechnet die kumulative Wahrscheinlichkeitsverteilung und ist insofern praktisch, da wir auf den Aufruf der Summenfunktion verzichten können. Die Verwendung von binom.cdf() ist wie folgt:
binom.cdf(k, n, p, loc). Auch hier lassen wir das Argument loc außer Acht und belassen es bei binom.cdf(k, n, p). Zusätzlich zu den Argumenten der Funktion binom.cdf() gilt zu beachten, dass binom.cdf() die Wahrscheinlichkeiten \(P(X≤x)\) wiedergibt und binom.sf(k, n, p) \(P(X>x)\) die Gegenwahrscheinlichkeit 1-binom.cdf().
Um dies zu verdeutlichen, lassen Sie uns \(P(X≤9)\) neu berechnen. Das Ergebnis der obigen Berechnung war \(0,81056\). Nun wenden wir die Funktion binom.cdf() an, um das gleiche Ergebnis zu erhalten.
binom.cdf(9, 25, 0.3)
0.8105639764950546
Um \(P(X>9)\) zu erhalten, was dasselbe ist wie \(1-P(X≤9)\), setzen wir das Argument
binom.sf(9, 25, 0.3)
0.18943602350494537
1 - binom.cdf(9, 25, 0.3)
0.18943602350494537
Um die binomische Wahrscheinlichkeitsverteilung zu visualisieren, verwenden wir die Funktion binom.rvs(), die Zufallsabweichungen für eine Binomialverteilung erzeugt, die durch ihre Größe \(n\) und die Erfolgs-/Misserfolgswahrscheinlichkeit \(p\) definiert ist.
# Setze random seed für Reproduzierbarkeit
np.random.seed(seed=42)
# Erzeuge y-Werte der Binomialverteilung
n = 25
p = 0.3
y = binom.rvs(n, p, size=2000)
# Erzeuge Plot
fig, ax = plt.subplots()
ax.set_xlim(-1, 26)
ax.set_title(f"Binomialverteilung: n={n} , p={p}")
ax.set_xlabel("Anzahl der Studenten die Prüfung bestehen")
ax.set_ylabel("Wahrscheinlichkeit (P=X)")
bins = max(y) - min(y)
_ = ax.hist(y, bins, edgecolor="k")
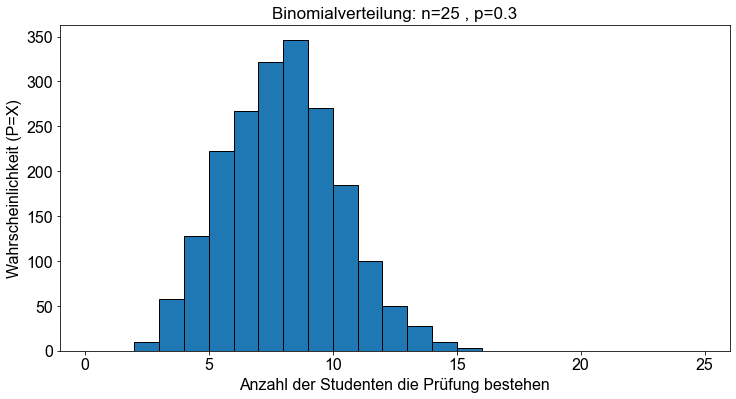
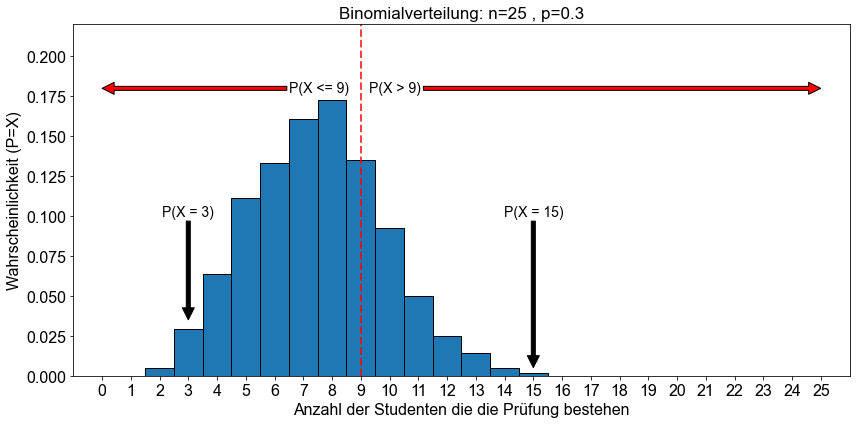
Zusätzlich visualisieren wir die oben diskutierten Wahrscheinlichkeiten: \(P(X=3), P(X=15), P(X≤9), P(X>9)\) und die entsprechende kumulative binomiale Wahrscheinlichkeitsverteilungsfunktion.
# Setze random seed für Reproduzierbarkeit
np.random.seed(seed=42)
# Erzeuge y-Werte der Binomialverteilung
n = 25
p = 0.3
y = binom.rvs(n, p, size=2000)
fig, ax = plt.subplots()
ax.set_xlim(-1, 26)
ax.set_ylim(0, 0.22)
ax.set_title(f"Binomialverteilung: n={n} , p={p}")
ax.set_xlabel("Anzahl der Studenten die die Prüfung bestehen")
ax.set_ylabel("Wahrscheinlichkeit (P=X)")
bins = max(y) - min(y)
ax.hist(y, bins, edgecolor="k", density=True, align="left")
ax.axvline(9, color="red", lw=2, linestyle="--", alpha=0.75)
ax.set_xticks(range(26))
# Annotation
ax.annotate(
"P(X > 9)",
xy=(25, 0.18),
xycoords="data",
xytext=(9.3, 0.18),
textcoords="data",
arrowprops=dict(facecolor="red", shrink=0.0005),
verticalalignment="center",
size=14,
)
ax.annotate(
"P(X <= 9)",
xy=(0, 0.18),
xycoords="data",
xytext=(6.5, 0.18),
textcoords="data",
arrowprops=dict(facecolor="red", shrink=0.0005),
verticalalignment="center",
size=14,
)
ax.annotate(
"P(X = 15)",
xy=(15, 0.005),
xycoords="data",
xytext=(15, 0.1),
textcoords="data",
arrowprops=dict(facecolor="black", shrink=0.0005),
horizontalalignment="center",
size=14,
)
ax.annotate(
"P(X = 3)",
xy=(3, 0.035),
xycoords="data",
xytext=(3, 0.1),
textcoords="data",
arrowprops=dict(facecolor="black", shrink=0.0005),
horizontalalignment="center",
size=14,
)
fig.tight_layout()
# Erzeuge x und y Werte für kumulitative Wahrscheinlichkeit
fig, ax = plt.subplots()
x = np.linspace(0, 25, num=26)
cdf = binom.cdf(x, n, p)
ax.plot(x, cdf, color="k", linewidth=3)
ax.set_xlim(-1, 26)
ax.set_ylim(-0.1, 1.1)
ax.set_title(f"Binomialverteilung: n = {n} , p = {p}")
ax.set_xlabel("Anzahl der Studenten die die Prüfung bestehen")
ax.set_ylabel("Kumulative Wahrscheinlichkeit")
ax.axvline(x=9, ymin=0, ymax=binom.cdf(9, n, p) * 0.95, color="red", linestyle="dashed")
ax.axhline(
y=binom.cdf(9, n, p),
xmin=0,
xmax=9 / 24.5,
color="red",
linestyle="dashed",
)
# Annotations
ax.annotate(
"P(X <= 9)",
xy=(9.2, 0.2),
xycoords="data",
xytext=(9.2, 0.2),
textcoords="data",
size=14,
)
ax.annotate(
"P(X <= 9) = 0.81)",
xy=(1.5, 0.85),
xycoords="data",
xytext=(1.5, 0.85),
textcoords="data",
size=14,
)
Text(1.5, 0.85, 'P(X <= 9) = 0.81)')
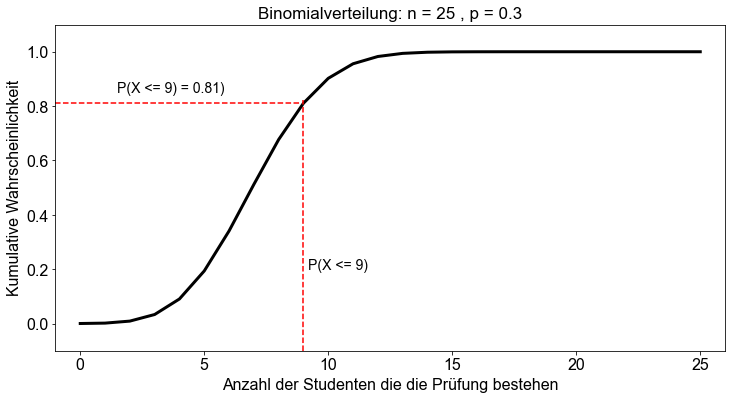
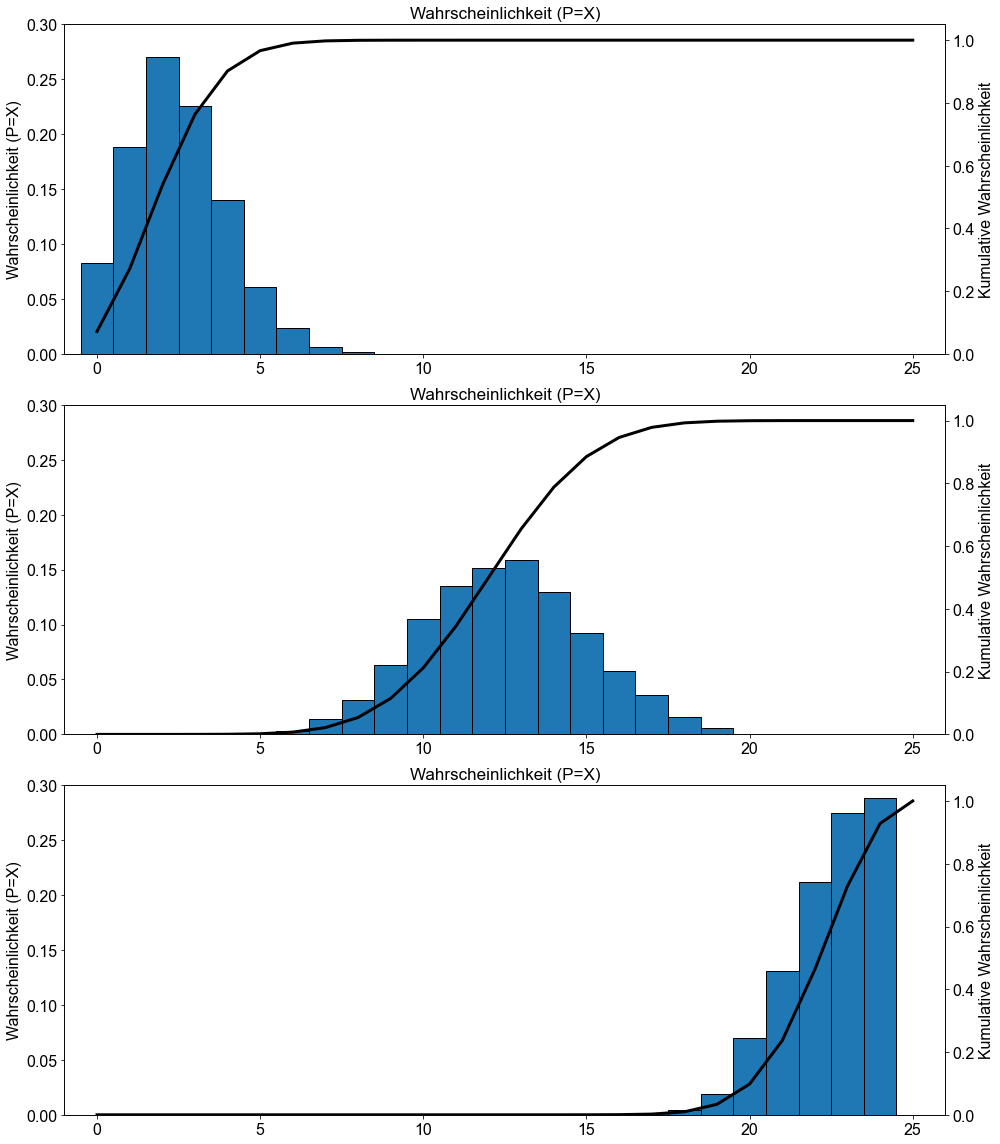
Zum Abschluss dieses Abschnitts und um Ihnen ein Gefühl für die Formen der verschiedenen binomischen Wahrscheinlichkeitsverteilungen zu vermitteln, werden im Folgenden drei verschiedene binomische Wahrscheinlichkeitsverteilungen und die entsprechenden kumulativen binomischen Beweisbarkeitsverteilungen für \(p=0,1, p=0,5\) und \(p=0,9\) angegeben.
fig, ax = plt.subplots(nrows=3, figsize=(14, 16))
x = np.linspace(0, 25, num=26)
for e, p in enumerate([0.1, 0.5, 0.9]):
y = binom.rvs(n, p, size=2000)
bins = max(y) - min(y)
ax[e].hist(y, bins, edgecolor="k", density=True, align="left")
ax[e].set_ylabel("Wahrscheinlichkeit (P=X)")
ax[e].set_title("Wahrscheinlichkeit (P=X)")
ax[e].set_xlim(-1, 26)
ax[e].set_ylim(0, 0.30)
# zweite Y-Achse
ax2 = ax[e].twinx()
cdf = binom.cdf(x, n, p)
ax2.plot(x, cdf, color="k", linewidth=3)
ax2.set_ylabel("Kumulative Wahrscheinlichkeit")
ax2.set_ylim(0, 1.05)
fig.tight_layout()
Mittelwert und Standardabweichung einer binomialen Zufallsvariable¶
Der Mittelwert und die Standardabweichung einer binomialen Zufallsvariablen mit den Parametern \(n\) und \(p\) sind jeweils
und
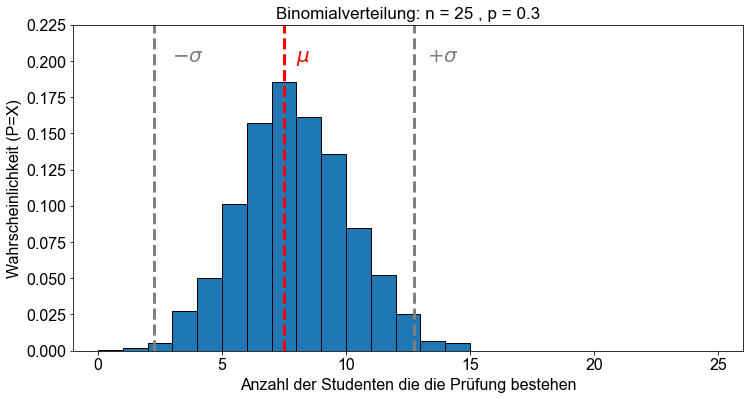
Erinnern wir uns an das Beispiel aus dem vorherigen Abschnitt. Die Wahrscheinlichkeit, die statistische Abschlussprüfung zu bestehen, beträgt \(0,3\). Wir betrachten eine Klasse mit \(25\) Studenten. Die Zufallsvariable \(X\), die dem Erfolg in der Prüfung entspricht, ist eine binomiale Zufallsvariable und folgt einer Binomialverteilung mit den Parametern \(n=25\) und \(p=0,3\). Somit können der Mittelwert μ und die Standardabweichung \(\sigma\) wie folgt berechnet werden:
und
Die folgende Grafik zeigt die Binomialverteilung mit den Parametern \(n=25\) und \(p=0,3\) sowie deren Mittelwert \(\mu\) und Standardabweichung \(\sigma\).
n = 25
p = 0.3
y = binom.rvs(n, p, size=2000)
mu = n * p
sigma = n * p * (1 - p)
fig, ax = plt.subplots()
bins = max(y) - min(y)
ax.hist(y, bins, edgecolor="k", density=True)
ax.set_ylim(0, 0.225)
ax.set_xlim(-1, 26)
ax.set_title(f"Binomialverteilung: n = {n} , p = {p}")
ax.set_xlabel("Anzahl der Studenten die die Prüfung bestehen")
ax.set_ylabel("Wahrscheinlichkeit (P=X)")
ax.axvline(mu, color="red", linewidth=3, linestyle="dashed")
ax.axvline(mu - sigma, color="grey", linewidth=3, linestyle="dashed")
ax.axvline(mu + sigma, color="grey", linewidth=3, linestyle="dashed")
# Annotation
ax.annotate("$\mu$", color="r", fontsize=20, xy=(7.5, 0.2), xytext=(8, 0.2))
ax.annotate("$-\sigma$", color="grey", fontsize=20, xy=(2.5, 0.2), xytext=(3, 0.2))
ax.annotate(
"$+\sigma$", color="grey", fontsize=20, xy=(12.75, 0.2), xytext=(13.25, 0.2)
)
Text(13.25, 0.2, '$+\\sigma$')
Binomiale Approximation der hypergeometrische Verteilung¶
Häufig möchte man den Anteil (Prozentsatz) der Mitglieder einer endlichen Grundgesamtheit bestimmen, die ein bestimmtes Attribut aufweisen. Im Allgemeinen ist die betrachtete Grundgesamtheit zu groß, als dass der Grundgesamtheitsanteil durch eine Zählung ermittelt werden könnte. Nehmen wir an, dass eine einfache Zufallsstichprobe des Umfangs \(n\) aus einer Grundgesamtheit entnommen wird, in der der Anteil der Mitglieder, die ein bestimmtes Merkmal aufweisen, \(p\) ist. Dann ist eine Zufallsvariable von primärer Bedeutung für die Schätzung von \(p\) die Anzahl der Mitglieder der Stichprobe, die das bestimmte Merkmal aufweisen, die wir als \(X\) bezeichnen.Die genaue Wahrscheinlichkeitsverteilung von \(X\) hängt davon ab, ob die Stichprobe mit oder ohne Ersetzung durchgeführt wird. Wird die Stichprobe mit Ersetzung durchgeführt, handelt es sich um Bernoulli-Versuche: Jede Auswahl eines Mitglieds der Grundgesamtheit entspricht einem Versuch. Ein Versuch ist erfolgreich, wenn das in diesem Versuch ausgewählte Mitglied das angegebene Attribut aufweist; andernfalls ist er nicht erfolgreich. Die Versuche sind unabhängig, da die Stichprobe mit Ersetzung durchgeführt wird. Die Erfolgswahrscheinlichkeit bleibt von Versuch zu Versuch gleich, sie ist immer gleich dem Anteil der Grundgesamtheit, der das angegebene Merkmal aufweist. Daher hat die Zufallsvariable \(X\) die Binomialverteilung mit den Parametern \(n\) (der Stichprobenumfang) und \(p\) (der Anteil der Grundgesamtheit) ([Papula, 2016] s.356).
In der Realität werden die Stichproben jedoch in der Regel ohne Ersetzung durchgeführt. Unter diesen Umständen handelt es sich bei dem Stichprobenverfahren nicht um Bernoulli-Versuche, da die Versuche nicht unabhängig sind und die Erfolgswahrscheinlichkeit von Versuch zu Versuch variiert. Mit anderen Worten: Die Zufallsvariable \(X\) hat keine Binomialverteilung. Ihre Verteilung wird als hypergeometrische Verteilung bezeichnet ([Papula, 2016] s.364).
In der Praxis kann eine hypergeometrische Verteilung jedoch in der Regel durch eine Binomialverteilung angenähert werden. Der Grund dafür ist, dass es bei einem Stichprobenumfang von nicht mehr als 5 % der Grundgesamtheit kaum einen Unterschied zwischen einer Stichprobe mit und ohne Ersatz gibt ([Papula, 2016] s.365).
Stichproben und die Binomialverteilung¶
Angenommen, eine einfache Zufallsstichprobe des Umfangs \(n\) wird aus einer endlichen Grundgesamtheit entnommen, in der der Anteil der Mitglieder, die ein bestimmtes Merkmal aufweisen, \(p\) ist. Dann hat die Anzahl der in der Stichprobe enthaltenen Mitglieder, die das bestimmte Merkmal aufweisen
eine exakte Binomialverteilung mit den Parametern \(n\) und \(p\), wenn die Stichprobe mit Ersatz durchgeführt wird
eine näherungsweise Binomialverteilung mit den Parametern \(n\) und \(p\) wenn die Stichprobenziehung ohne Ersetzung erfolgt und der Stichprobenumfang nicht mehr als \(5 \%\) des Grundgesamtheitsumfangs beträgt ([Papula, 2016] s.365).
