Die Normalverteilung
Contents
Die Normalverteilung¶
Welche Kenngrößen charakterisieren die Normalverteilung
Was ist die Standardnormalverteilung und in welchem Bezug steht sie zur Normalverteilung?
Generieren Sie \(10.000\) Zufallswerte für die Normalverteilung mit Mittelwert \(\mu = 1\) und Standardabweichung \(\sigma = 3\), unter Verwendung der Funktion
np.random.normal(loc, scale, size), und stellen Sie das Ergebnis als Histogramm dar.Führen Sie eine \(z\)-Transformation für diese Werte durch und plotten Sie das Ergebnis.
# Frage 3 ...
# Frage 4 ...
Lösungen¶
Die Normalverteilung wird durch ihren Mittelwert \(\mu\) und ihre Standardabweichung \(\sigma\) beschrieben. \(X \sim N( \mu, \sigma)\)
Die Standardnormalverteilung ist die Normalverteilung mit Mittelwert \(\mu=0\) und Standardabweichung \(\sigma=1\). Sie entspricht also der Normalverteilung mit \(X \sim N( 0, 1)\). Durch die Anwendung der \(z\)-Transformation \(z = \frac{x-\mu}{\sigma}\) können beliebige Normalverteilungen auf die Standardnormalverteilung abgebildet werden.
import numpy as np
import matplotlib.pyplot as plt
loc = 2
scale = 3
size = 10000
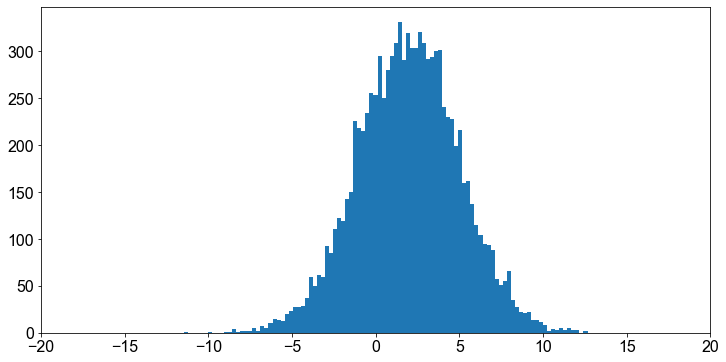
data = np.random.normal(loc=loc, scale=scale, size=size)
x = np.linspace(-20, 20, size)
fig, ax = plt.subplots()
ax.hist(data, bins=100)
ax.set_xlim(-20, 20)
plt.show()
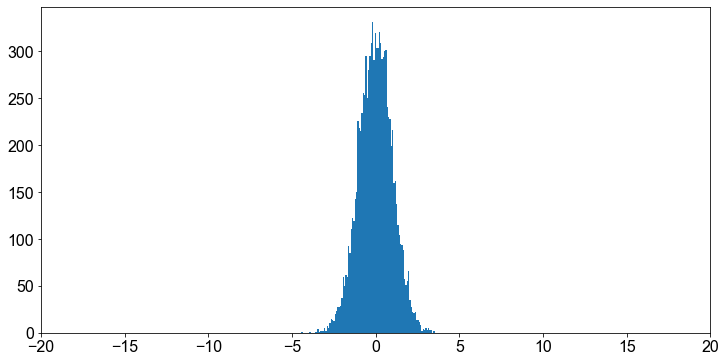
z = (data - np.mean(data)) / np.std(data)
fig, ax = plt.subplots()
ax.hist(z, bins=100)
ax.set_xlim(-20, 20)
plt.show()