Streuungsmaße
Contents
Streuungsmaße¶
import random
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import norm, gaussian_kde
Die Maße der zentralen Tendenz, wie Mittelwert, Median und Modus, geben nicht das ganze Bild der Verteilung eines Datensatzes wieder. Zwei Datensätze mit demselben Mittelwert können völlig unterschiedliche Streuungen aufweisen. Die Streuung der Beobachtungswerte des einen Datensatzes kann viel größer oder kleiner sein als die des anderen Datensatzes. Daher ist der Mittelwert, Median oder Modus allein in der Regel kein ausreichendes Maß, um die Form der Verteilung eines Datensatzes aufzuzeigen. Wir benötigen auch ein Maß, das Informationen über die Variation zwischen den Datenwerten liefert. Diese Maße werden als Streuungsmaße bezeichnet. Die Maße der zentralen Tendenz und der Streuung ergeben zusammengenommen ein besseres Bild eines Datensatzes als die Maße der zentralen Tendenz allein ([Fahrmeir et al., 2016] s.65).
Varianz und Standardabweichung¶
Die Varianz ist die Summe der quadrierten Abweichungen vom Mittelwert. Die Varianz für Populationsdaten wird mit \(\sigma^2\) bezeichnet (gelesen als Sigma-Quadrat), und die für Stichprobendaten berechnete Varianz wird mit \(s^2\) bezeichnet.
und $\( s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1} \)$
wobei \(\sigma^2\) die Varianz der Grundgesamtheit und \(s^2\) die Stichprobenvarianz ist. Die Größe \(x_i-\mu\) oder \(x_i-\bar{x}\) in den obigen Formeln wird als die Abweichung des \(x_i\)-Wertes \((x_1,x_2, \dots ,x_n)\) vom Mittelwert bezeichnet ([Fahrmeir et al., 2016] s.64).
Die Standardabweichung ist das gebräuchlichste Maß für die Streuung. Der Wert der Standardabweichung gibt an, wie eng die Werte eines Datensatzes um den Mittelwert herum gestreut sind. Im Allgemeinen zeigt ein niedriger Wert der Standardabweichung für einen Datensatz an, dass die Werte dieses Datensatzes über einen relativ kleineren Bereich um den Mittelwert herum verteilt sind. Im Gegensatz dazu zeigt ein größerer Wert der Standardabweichung für einen Datensatz an, dass die Werte dieses Datensatzes über einen relativ größeren Bereich um den Mittelwert herum gestreut sind ([Fahrmeir et al., 2016] s.65).
import matplotlib.pyplot as plt
TITLESIZE = 17
SEED = np.random.seed(42)
SIZE = 100
x = np.linspace(0, 1, SIZE)
fig, ax = plt.subplots(ncols=2, figsize=(16, 6))
y = np.random.normal(loc=0.5, scale=1.0, size=SIZE)
ax[0].plot(x, y, "o")
ax[0].set_title("Geringe Abweichungen um den Mittelwert", size=TITLESIZE)
y = np.random.normal(loc=0.5, scale=3.0, size=SIZE)
ax[1].plot(x, y, "o")
ax[1].set_title("Grosse Abweichungen um den Mittelwert", size=TITLESIZE)
for _ax in ax:
_ax.set_xticks([])
_ax.set_yticks([])
_ax.axhline(0.5, color="k")
_ax.set_ylim(-6, 6)
_ax.legend(["Daten", "Mittelwert"])
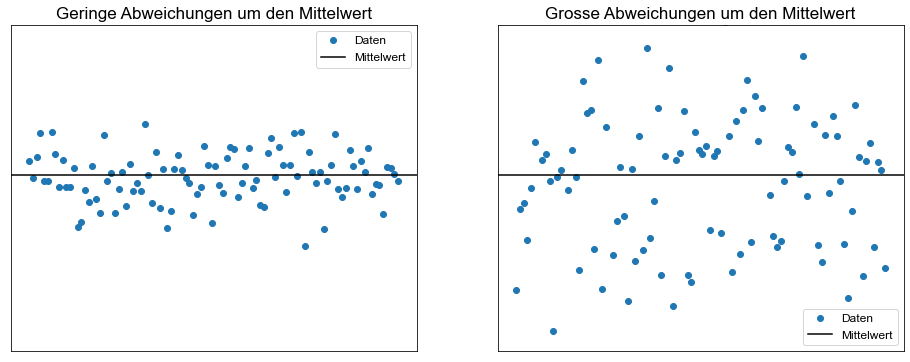
Die Standardabweichung erhält man durch Ziehen der Quadratwurzel aus der Varianz. Folglich wird die für Grundgesamtheitsdaten berechnete Standardabweichung mit \(\sigma\) und die für Stichprobendaten berechnete Standardabweichung mit \(s\) bezeichnet.
und
wobei \(\sigma\) die Standardabweichung der Grundgesamtheit und \(s\) die Standardabweichung der Stichprobe ist.
Als Übung berechnen wir für einige numerische Variablen, die im students Datensatz von Interesse sind, den Mittelwert, den Median, die Varianz und die Standardabweichung und stellen sie in einem Dataframe dar.
# Lesen der Datei students.csv als Dataframe; nur die Spalten "age", "weight", "height" und "nc.score" Spalten werden eingelesen
students = pd.read_csv(
"../../data/students.csv",
index_col=0,
usecols=["age", "height", "weight", "nc.score"],
)
# Zeige die ersten 10 Werte
students.head(10)
| age | height | weight | nc.score | |
|---|---|---|---|---|
| 1 | 19 | 160 | 64.8 | 1.91 |
| 2 | 19 | 172 | 73.0 | 1.56 |
| 3 | 22 | 168 | 70.6 | 1.24 |
| 4 | 19 | 183 | 79.7 | 1.37 |
| 5 | 21 | 175 | 71.4 | 1.46 |
| 6 | 19 | 189 | 85.8 | 1.34 |
| 7 | 21 | 156 | 65.9 | 1.11 |
| 8 | 21 | 167 | 65.7 | 2.03 |
| 9 | 18 | 195 | 94.4 | 1.29 |
| 10 | 18 | 165 | 66.0 | 1.19 |
Pandas verfügt über die Methode agg. Diese lässt uns sehr einfach verschiedene deskritptive Statisitken berechnen.
students.agg(["mean", "median", "var", "std"])
| age | height | weight | nc.score | |
|---|---|---|---|---|
| mean | 22.541571 | 171.380750 | 72.998131 | 2.166481 |
| median | 21.000000 | 171.000000 | 71.800000 | 2.040000 |
| var | 36.785568 | 122.711652 | 74.566017 | 0.658610 |
| std | 6.065111 | 11.077529 | 8.635162 | 0.811548 |
Verwendung der Standardabweichung¶
Mit Hilfe des Mittelwerts und der Standardabweichung lässt sich der Anteil oder Prozentsatz der Gesamtbeobachtungen ermitteln, die in ein bestimmtes Intervall um den Mittelwert fallen.
Tschebyscheff-Theorem¶
Das Tschebyscheff Ungleichung gibt eine untere Schranke für die Fläche unter einer Kurve zwischen zwei Punkten, die auf gegenüberliegenden Seiten des Mittelwerts und im gleichen Abstand vom Mittelwert liegen.
Für jede Zahl \(k\), die größer als \(1\) ist, liegen mindestens \(1-\frac{1}{k^2}\) der Datenwerte innerhalb von \(k\) Standardabweichungen vom Mittelwert.
Lassen Sie uns Python verwenden, um ein Gefühl für den Tschebyscheff-Theorem zu bekommen.
k = np.arange(1, 4.1, 0.1)
value = np.round((1 - (1 / k**2)) * 100)
chebyshev = pd.DataFrame({"k": k, "Prozent": value})
chebyshev
| k | Prozent | |
|---|---|---|
| 0 | 1.0 | 0.0 |
| 1 | 1.1 | 17.0 |
| 2 | 1.2 | 31.0 |
| 3 | 1.3 | 41.0 |
| 4 | 1.4 | 49.0 |
| 5 | 1.5 | 56.0 |
| 6 | 1.6 | 61.0 |
| 7 | 1.7 | 65.0 |
| 8 | 1.8 | 69.0 |
| 9 | 1.9 | 72.0 |
| 10 | 2.0 | 75.0 |
| 11 | 2.1 | 77.0 |
| 12 | 2.2 | 79.0 |
| 13 | 2.3 | 81.0 |
| 14 | 2.4 | 83.0 |
| 15 | 2.5 | 84.0 |
| 16 | 2.6 | 85.0 |
| 17 | 2.7 | 86.0 |
| 18 | 2.8 | 87.0 |
| 19 | 2.9 | 88.0 |
| 20 | 3.0 | 89.0 |
| 21 | 3.1 | 90.0 |
| 22 | 3.2 | 90.0 |
| 23 | 3.3 | 91.0 |
| 24 | 3.4 | 91.0 |
| 25 | 3.5 | 92.0 |
| 26 | 3.6 | 92.0 |
| 27 | 3.7 | 93.0 |
| 28 | 3.8 | 93.0 |
| 29 | 3.9 | 93.0 |
| 30 | 4.0 | 94.0 |
Um es in Worte zu fassen: Für \(k=2\) bedeutet das, dass mindestens \(75 \% \) der Datenwerte innerhalb von 2 Standardabweichungen vom Mittelwert liegen.
Stellen wir das Tschebyscheff-Theorem mit Python dar:
fig, ax = plt.subplots()
chebyshev.plot.scatter(x="k", y="Prozent", ax=ax)
ax.set_title("Tschebyscheff-Theorem")
ax.grid()
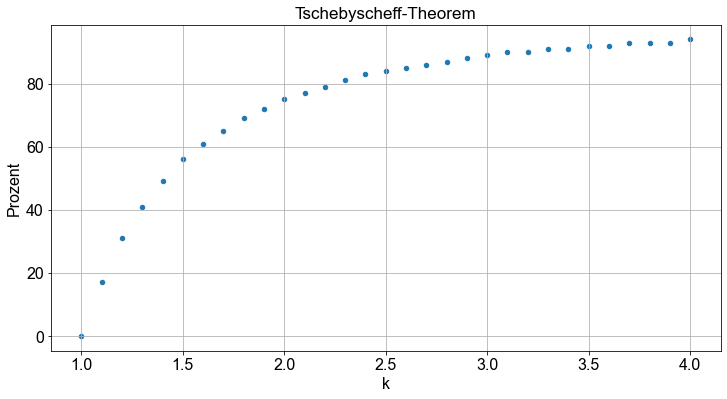
Das Theorem gilt sowohl für Stichproben- als auch für Grundgesamtheitsdaten. Das Tschebyscheffsche Ungleichung gilt für Verteilungen beliebiger Form. Es kann jedoch nur für \(k > 1\) verwendet werden. Denn wenn \(k=1\) ist, ist der Wert von \(1-\frac{1}{k^2}\) Null, und wenn \(k < 1\) ist, ist der Wert von \(1-\frac{1}{k^2}\) negativ ([Fahrmeir et al., 2016] s.304).
Empirische Regel¶
Während das Tschebyscheffsche Ungleichung auf jede Art von Verteilung anwendbar ist, gilt die empirische Regel nur für eine bestimmte Art von Verteilung, die so genannte Gaußverteilung oder Normalverteilung. Es gibt 3 Regeln:
Bei einer Normalverteilung sind
\(68 \%\) der Beobachtungen innerhalb einer Standardabweichung des Mittelwerts.
\(95 \%\) der Beobachtungen innerhalb von zwei Standardabweichungen des Mittelwerts.
\(99,7 \%\) der Beobachtungen innerhalb von drei Standardabweichungen des Mittelwerts.
Da wir inzwischen über genügend Hacking-Power verfügen, werden wir versuchen zu testen, ob die drei Regeln gültig sind.
(1) Erstens werden wir die Funktion random.normal() in Python erforschen, um normalverteilte Daten zu erzeugen, und
(2) Zweitens werden wir zu unserem students Datensatz zurückkehren und diese Regeln an diesem Datensatz zu validieren.
Die Normalverteilung gehört zur Familie der stetigen Verteilungen. In Python gibt es eine Vielzahl von Wahrscheinlichkeitsverteilungen (hier). Um Daten aus einer Normalverteilung zu erzeugen, kann man die Funktion random.normal() verwenden, die ein Zufallsvariablengenerator für die Normalverteilung ist.
Mit der Funktion np.random.normal(loc=0.0, scale=1.0) können wir Zufallsvariablen aus einer Normalverteilung mit einem gegebenen Mittelwert (Standard ist \(0\)) und einer Standardabweichung (Standard ist \(1\)) entnehmen. Mit dem Argument size können wir die Anzahl der erzeugten Zufallsvariablen bestimmen.
np.random.normal(loc=0.0, scale=1.0, size=1)
array([0.35778736])
np.random.normal(loc=0.0, scale=1.0, size=1)
array([0.56078453])
np.random.normal(loc=0.0, scale=1.0, size=1)
array([1.08305124])
Wir können die Funktion ziemlich einfach bitten, Hunderte oder Tausende oder noch mehr (Pseudo-)Zufallszahlen zu ziehen:
np.random.normal(loc=0.0, scale=1.0, size=10)
array([ 1.05380205, -1.37766937, -0.93782504, 0.51503527, 0.51378595,
0.51504769, 3.85273149, 0.57089051, 1.13556564, 0.95400176])
np.random.normal(loc=0.0, scale=1.0, size=100)
array([ 0.65139125, -0.31526924, 0.75896922, -0.77282521, -0.23681861,
-0.48536355, 0.08187414, 2.31465857, -1.86726519, 0.68626019,
-1.61271587, -0.47193187, 1.0889506 , 0.06428002, -1.07774478,
-0.71530371, 0.67959775, -0.73036663, 0.21645859, 0.04557184,
-0.65160035, 2.14394409, 0.63391902, -2.02514259, 0.18645431,
-0.66178646, 0.85243333, -0.79252074, -0.11473644, 0.50498728,
0.86575519, -1.20029641, -0.33450124, -0.47494531, -0.65332923,
1.76545424, 0.40498171, -1.26088395, 0.91786195, 2.1221562 ,
1.03246526, -1.51936997, -0.48423407, 1.26691115, -0.70766947,
0.44381943, 0.77463405, -0.92693047, -0.05952536, -3.24126734,
-1.02438764, -0.25256815, -1.24778318, 1.6324113 , -1.43014138,
-0.44004449, 0.13074058, 1.44127329, -1.43586215, 1.16316375,
0.01023306, -0.98150865, 0.46210347, 0.1990597 , -0.60021688,
0.06980208, -0.3853136 , 0.11351735, 0.66213067, 1.58601682,
-1.2378155 , 2.13303337, -1.9520878 , -0.1517851 , 0.58831721,
0.28099187, -0.62269952, -0.20812225, -0.49300093, -0.58936476,
0.8496021 , 0.35701549, -0.6929096 , 0.89959988, 0.30729952,
0.81286212, 0.62962884, -0.82899501, -0.56018104, 0.74729361,
0.61037027, -0.02090159, 0.11732738, 1.2776649 , -0.59157139,
0.54709738, -0.20219265, -0.2176812 , 1.09877685, 0.82541635])
Wenn wir ein Histogramm dieser Zahlen erstellen, sehen wir die namensgebende glockenförmige Verteilung.
y_norm = np.random.normal(loc=0.0, scale=1.0, size=100000)
bins = int(len(y_norm) / 1000) # bestimmt die Anzahl der Bins
plt.hist(y_norm, bins=bins)
plt.ylabel("Absolute Häufigkeit")
plt.show()
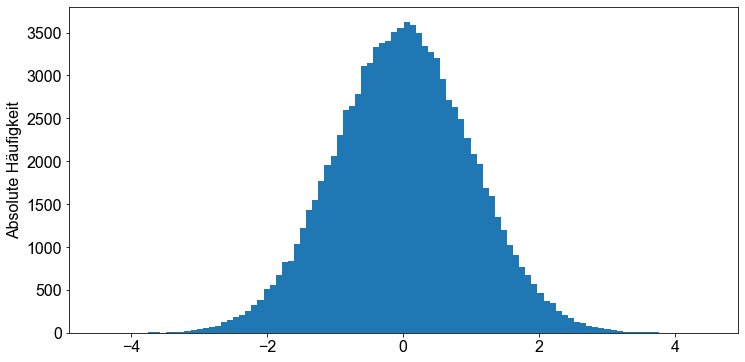
Wir kennen bereits den Mittelwert und die Standardabweichung der Werte in y_norm, da wir die Funktion np.random.normal() explizit mit mean=0 und sd=1 aufgerufen haben. Wir müssen also nur die Zahlen in y_norm zählen, die größer als \(-1\) bzw. kleiner als \(1\) und \(2\) bzw. \(-2\) und \(3\) bzw. \(-3\) sind, und sie zur Länge von y_norm, in unserem Fall \(100.000\), in Beziehung setzen, um die drei oben genannten Regeln zu bestätigen.
# Berechne Anzahl der Werte < 1 - Anzahl der Werte > -1 durch Gesamtanzahl
sd1 = sum((y_norm > -1) & (y_norm < 1)) / len(y_norm)
# Berechne Anzahl der Werte < 2 - Anzahl der Werte > -2 durch Gesamtanzahl
sd2 = sum((y_norm > -2) & (y_norm < 2)) / len(y_norm)
# Berechne Anzahl der Werte < 3 - Anzahl der Werte > -3 durch Gesamtanzahl
sd3 = sum((y_norm > -3) & (y_norm < 3)) / len(y_norm)
print("sd1 :", sd1)
print("sd2 :", sd2)
print("sd3 :", sd3)
sd1 : 0.68143
sd2 : 0.95444
sd3 : 0.99737
Perfekte Übereinstimmung! Die drei empirischen Regeln sind offensichtlich gültig. Um unsere Ergebnisse zu veranschaulichen, stellen wir das Histogramm erneut dar und fügen einige Anmerkungen hinzu. Bitte beachten Sie, dass wir in der hist()-Funktion das Argument density=True setzen. Dies hat zur Folge, dass das resultierende Histogramm nicht mehr die Zählungen auf der y-Achse anzeigt, sondern die Dichtewerte (normalisierte Zählung geteilt durch Bin-Breite), was bedeutet, dass sich die Balkenbereiche zu \(1\) summieren.
fig, ax = plt.subplots()
ax.hist(y_norm, bins=bins)
ax.set_ylabel("Absolute Häufigkeit")
for e, std in enumerate([(-1, 1), (-2, 2), (-3, 3)]):
plt.axvline(std[0], color=f"C{e+1}")
plt.axvline(std[1], color=f"C{e+1}")
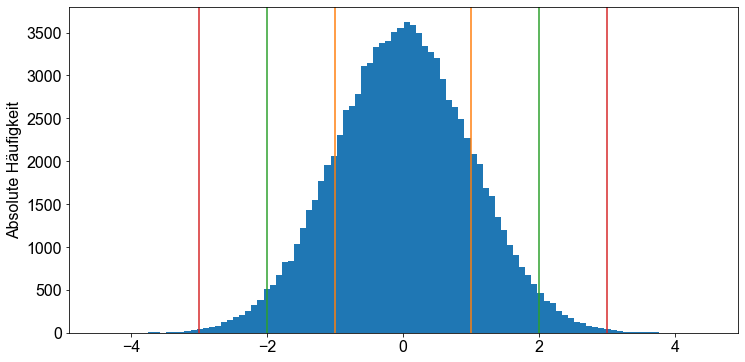
Nun, lassen Sie uns an der zweiten Aufgabe arbeiten: Überprüfen Sie die drei empirischen Regeln anhand des students Datensatzes. Dazu müssen wir überprüfen, ob eine der numerischen Variablen im Studentendatensatz normalverteilt ist. Wir beginnen mit der Extraktion numerischer Variablen von Interesse aus dem students Datensatz. Dann zeichnen wir Histogramme und beurteilen, ob die Variable normalverteilt ist oder nicht. Zunächst überprüfen wir jedoch den Datensatz, indem wir die Funktion head() aufrufen.
# Lesen der Datei students.csv als Dataframe;
students = pd.read_csv(
"../../data/students.csv",
usecols=["age", "height", "weight", "score1", "score2", "salary"],
)
students.head(10)
| age | height | weight | score1 | score2 | salary | |
|---|---|---|---|---|---|---|
| 1 | 19 | 160 | 64.8 | NaN | NaN | NaN |
| 2 | 19 | 172 | 73.0 | NaN | NaN | NaN |
| 3 | 22 | 168 | 70.6 | 45.0 | 46.0 | NaN |
| 4 | 19 | 183 | 79.7 | NaN | NaN | NaN |
| 5 | 21 | 175 | 71.4 | NaN | NaN | NaN |
| 6 | 19 | 189 | 85.8 | NaN | NaN | NaN |
| 7 | 21 | 156 | 65.9 | NaN | NaN | NaN |
| 8 | 21 | 167 | 65.7 | 58.0 | 62.0 | NaN |
| 9 | 18 | 195 | 94.4 | 57.0 | 67.0 | NaN |
| 10 | 18 | 165 | 66.0 | NaN | NaN | NaN |
Um einen Überblick über die Form der Verteilung der einzelnen Variablen zu erhalten, verwenden wir die Methode hist().
cols = students.columns
fig, ax = plt.subplots(ncols=int(len(cols) / 2), nrows=2)
ax = np.ravel(ax) # vereinfacht das iterieren durch die axes Objekte
titles = {
"age": "Alter",
"height": "Grösse",
"weight": "Gewicht",
"score1": "Punkte1",
"score2": "Punkte2",
"salary": "Gehalt",
}
for e, col in enumerate(cols):
bins = int(students[col].nunique() / 2)
ax[e].hist(students[col], bins=bins, density=True)
ax[e].set_title(titles[col])
fig.tight_layout()
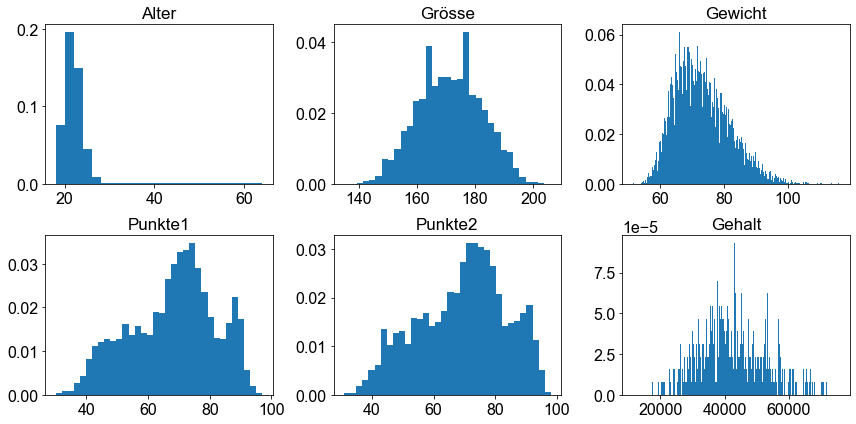
Wir stellen sofort fest, dass einige Variablen positiv verzerrt sind, also schließen wir sie aus und behalten diejenigen, die normal verteilt zu sein scheinen.
cols = ["height", "salary"]
fig, ax = plt.subplots(ncols=2)
ax = np.ravel(ax) # vereinfacht das iterieren durch die axes Objekte
bins_fact = {"height": 2, "salary": 40}
for e, col in enumerate(cols):
bins = int(students[col].nunique() / bins_fact[col])
ax[e].hist(students[col], bins=bins)
ax[e].set_title(titles[col])
fig.tight_layout()
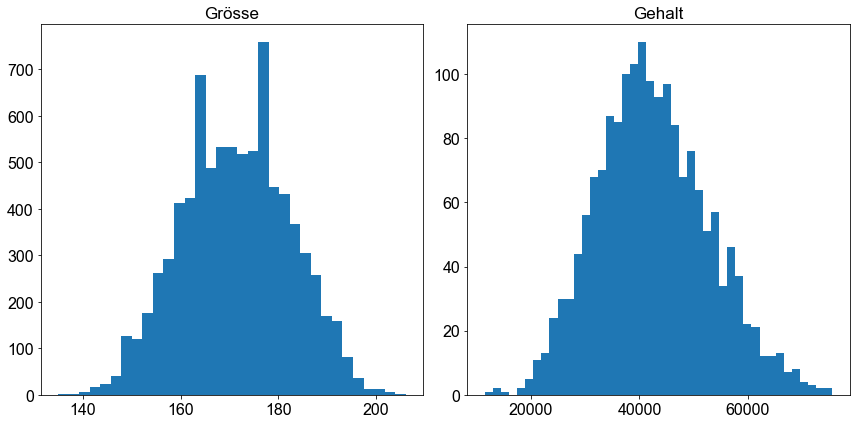
Nun, sowohl die Variable height als auch die Variable salary scheinen mehr oder weniger normalverteilt zu sein. Es ist also eine Frage des Geschmacks, welche Variable man für die weitere Analyse auswählt. Für den Moment bleiben wir bei der Gehaltsvariable und überprüfen, ob die drei oben genannten empirischen Regeln gültig sind. Wir wechseln zu Python und validieren diese Regeln, indem wir zunächst den Mittelwert und die Standardabweichungen berechnen. Bitte beachten Sie, dass die Gehaltsvariable Fehlwerte enthält, die mit NA gekennzeichnet sind. Daher schließen wir zunächst alle NA-Werte aus, indem wir die Funktion dropna() anwenden.
salary = students["salary"].dropna()
salary
11 45254.108021
13 40552.790243
14 27007.030294
17 33969.159268
28 50617.641870
...
8229 33259.703079
8234 41028.241341
8235 36750.087135
8238 40112.041834
8239 45900.134459
Name: salary, Length: 1753, dtype: float64
print(f"Mittelwert des Gehalts: {salary.mean()}")
print(f"1 Standardabweichung des Gehalts: {salary.std()}")
print(f"2 Standardabweichungen des Gehalts: {2 * salary.std()}")
print(f"3 Standardabweichungen des Gehalts: {3 * salary.std()}")
Mittelwert des Gehalts: 42522.112364224806
1 Standardabweichung des Gehalts: 10333.139905546619
2 Standardabweichungen des Gehalts: 20666.279811093238
3 Standardabweichungen des Gehalts: 30999.41971663986
Wie in der obigen allgemeinen Beispielform zählen wir die Anzahl der Werte, die größer als \(+1\) s.d. bzw. kleiner als \(-1\) s.d. und \(+2\) s.d. bzw. \(-2\) s.d. und \(+3\) s.d. bzw. \(-3\) s.d. sind, und setzen sie in Beziehung zur Länge des Vektors, in unserem Fall \(1753\).
salary_mean = salary.mean()
salary_std = salary.std()
sd1 = (
sum((salary > (salary_mean - salary_std)) & (salary < (salary_mean + salary_std)))
/ salary.shape[0]
)
sd2 = (
sum(
(salary > (salary_mean - 2 * salary_std))
& (salary < (salary_mean + 2 * salary_std))
)
/ salary.shape[0]
)
sd3 = (
sum(
(salary > (salary_mean - 3 * salary_std))
& (salary < (salary_mean + 3 * salary_std))
)
/ salary.shape[0]
)
print("sd1 :", sd1)
print("sd2 :", sd2)
print("sd3 :", sd3)
sd1 : 0.6708499714774672
sd2 : 0.9560752994865944
sd3 : 0.9977181973759269
Wow, ziemlich nah dran! Offensichtlich zeigt die Gehaltsvariable eine starke Tendenz zur Unterstützung der so genannten empirischen Regel. Wir stellen das Histogramm für die Variable salary dar, um unseren Eindruck zu bestätigen.
fig, ax = plt.subplots()
bins = int(salary.nunique() / 40)
ax.hist(salary, bins=bins)
ax.set_ylabel("Absolute Häufigkeit")
ax.set_xlabel("Gehalt")
for e in range(3):
ax.axvline(salary_mean + (e + 1) * salary_std, color=f"C{e+1}")
ax.axvline(salary_mean - (e + 1) * salary_std, color=f"C{e+1}")
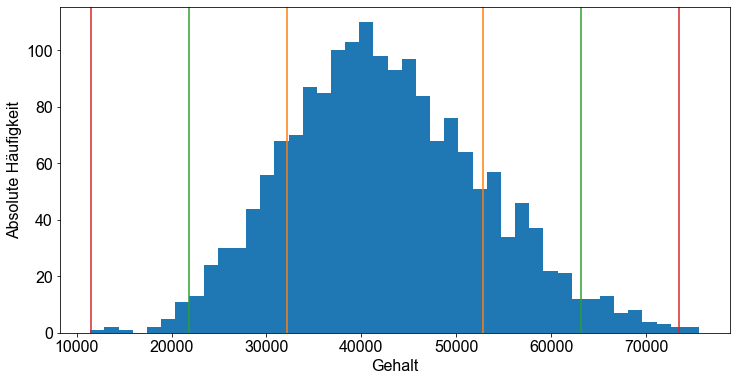
Wir können nun unseren Visualisierungsansatz erweitern, indem wir die empirische Dichteschätzung mit der Funktion scipy_kernel.evaluate() grafisch darstellen und ihre Form überprüfen. Wir stellen die empirische Dichteschätzung als gestrichelte Linie dar, indem wir das (Linientyp-Argument) '-.' und eine Linienbreite von \(3\) (Argument linewidth=3.0) setzen.
fig, ax = plt.subplots()
bins = int(salary.nunique() / 40)
ax.hist(salary, bins=bins, density=True)
ax.set_ylabel("Dichte")
ax.set_xlabel("Gehalt")
# empirische Dichteschätzung
x_salary = np.linspace(salary.min(), salary.max(), 100)
scipy_kernel = gaussian_kde(salary)
dens_emp = scipy_kernel.evaluate(x_salary)
ax.plot(x_salary, dens_emp, color="k", linestyle="dashed", linewidth=3.0)
# Standardabweichungen
for e in range(3):
ax.axvline(salary_mean + (e + 1) * salary_std, color=f"C{e+1}")
ax.axvline(salary_mean - (e + 1) * salary_std, color=f"C{e+1}")
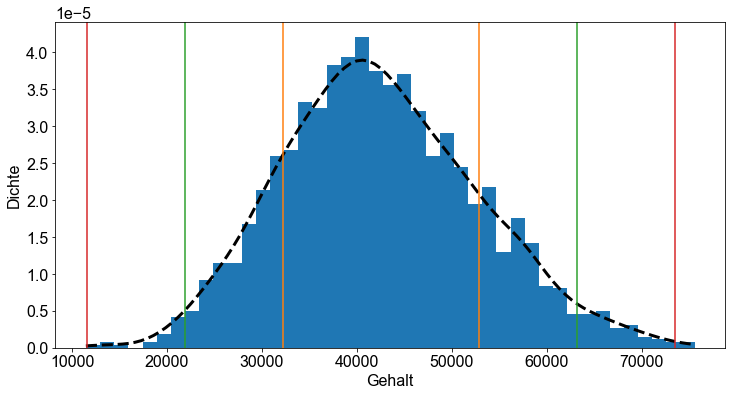
Schließlich vergleichen wir unsere empirische Dichteschätzung mit der theoretischen Wahrscheinlichkeitsdichtefunktion, die auf dem tatsächlichen Mittelwert und der Standardabweichung der Daten salary basiert. Für einen besseren visuellen Vergleich wechseln wir zurück zu einer nicht eingefärbten Histogramm-Darstellung.
fig, ax = plt.subplots()
bins = int(salary.nunique() / 40)
ax.hist(salary, bins=bins, density=True)
ax.set_ylabel("Dichte")
ax.set_xlabel("Gehalt")
# empirische Dichteschätzung
x_salary = np.linspace(salary.min(), salary.max(), 100)
scipy_kernel = gaussian_kde(salary)
dens_emp = scipy_kernel.evaluate(x_salary)
ax.plot(
x_salary,
dens_emp,
color="k",
linestyle="dashed",
linewidth=3.0,
label="Empirische Dichteschätzung",
)
# Wahrscheinlichkeitsdichtefunktion
pdf = norm.pdf(x_salary, loc=salary.mean(), scale=salary.std())
ax.plot(
x_salary, pdf, color="k", linewidth=3.0, label="Wahrscheinlichkeitsdichtefunktion"
)
# Standardabweichungen
for e in range(3):
ax.axvline(salary_mean + (e + 1) * salary_std, color=f"C{e+1}")
ax.axvline(salary_mean - (e + 1) * salary_std, color=f"C{e+1}")
ax.legend()
<matplotlib.legend.Legend at 0x170432380>
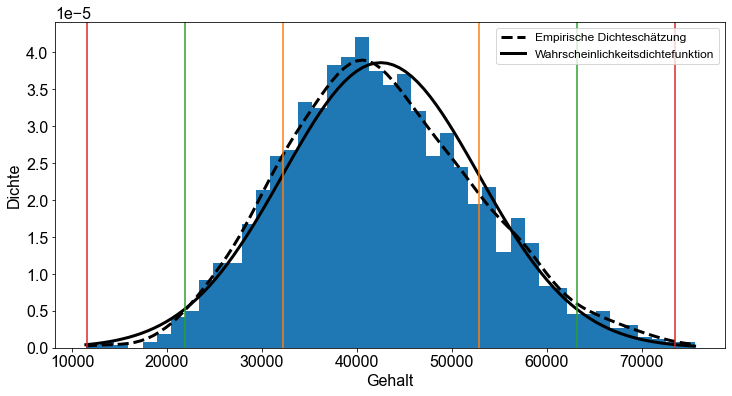
Wir können daraus schließen, dass salary im Datensatz der students ungefähr normalverteilt ist. Die Grafik zeigt jedoch, dass die Verteilung der Gehaltsvariablen leicht nach linksschief ist. Dies ist an der Abweichung zwischen der empirischen Dichteschätzung und der Wahrscheinlichkeitsdichtefunktion zu erkennen.
Die Spannweite¶
Die Spannweite als Maß für die Streuung ist einfach zu berechnen. Sie ergibt sich aus der Differenz zwischen dem größten und dem kleinsten Wert in einem Datensatz.
Betrachten wir unseren students Datensatz. Wir unterteilen den Datensatz so, dass er nur numerische Daten enthält.
df = pd.read_csv("../../data/students.csv")
df.sample(10)
| stud.id | name | gender | age | height | weight | religion | nc.score | semester | major | minor | score1 | score2 | online.tutorial | graduated | salary | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3600 | 255883 | Morrison-Cook, Austin | Male | 20 | 172 | 72.6 | Other | 1.67 | 4th | Mathematics and Statistics | Economics and Finance | 91.0 | 87.0 | 0 | 0 | NaN |
| 2082 | 686345 | Lenahan, Kyle | Male | 21 | 181 | 78.0 | Other | 1.38 | 2nd | Social Sciences | Economics and Finance | NaN | NaN | 0 | 0 | NaN |
| 522 | 346731 | Lee, Nicholas | Male | 22 | 192 | 93.1 | Catholic | 1.27 | 5th | Environmental Sciences | Social Sciences | 78.0 | 65.0 | 1 | 1 | 49068.502177 |
| 5604 | 963305 | Kramer, David | Male | 56 | 170 | 72.6 | Orthodox | 2.14 | 5th | Environmental Sciences | Mathematics and Statistics | 72.0 | 71.0 | 1 | 1 | 42606.347228 |
| 3671 | 124687 | Than, Jonathan | Male | 22 | 172 | 72.4 | Protestant | 1.79 | 4th | Environmental Sciences | Mathematics and Statistics | 62.0 | 69.0 | 0 | 1 | 49004.727119 |
| 5376 | 696262 | Macasinag, Paulo | Male | 20 | 197 | 94.3 | Catholic | 3.41 | 6th | Political Science | Environmental Sciences | 51.0 | 47.0 | 1 | 1 | 39442.803935 |
| 2318 | 452190 | Briseno, Alisha | Female | 63 | 162 | 68.0 | Catholic | 2.19 | 2nd | Mathematics and Statistics | Environmental Sciences | NaN | NaN | 0 | 0 | NaN |
| 4840 | 955228 | Thapa, Richard | Male | 23 | 175 | 76.0 | Other | 2.48 | 1st | Mathematics and Statistics | Environmental Sciences | NaN | NaN | 0 | 0 | NaN |
| 1286 | 854649 | Duling, Joshua Ian | Male | 61 | 170 | 70.3 | Protestant | 1.54 | >6th | Economics and Finance | Mathematics and Statistics | 64.0 | 69.0 | 1 | 0 | NaN |
| 118 | 582922 | Valenciano-Poffenbarger, Quincie | Female | 19 | 175 | 76.8 | Catholic | 2.19 | 1st | Social Sciences | Mathematics and Statistics | NaN | NaN | 0 | 0 | NaN |
Wir sind also an den Kategorien age, height, weight und nc.score interessiert. Wir verwenden die Methoden min() und max(), um das Minimum und Maximum der ausgewählten Variablen zu berechnen. Erneut greifen wir auf die agg-Methode zurück.
summary = df[["age", "height", "weight", "nc.score"]].agg(["min", "max"])
summary
| age | height | weight | nc.score | |
|---|---|---|---|---|
| min | 18 | 135 | 51.4 | 1.0 |
| max | 64 | 206 | 116.0 | 4.0 |
Um nun die Spannweite für jede Variable zu berechnen, müssen wir nur eine Zeile von der anderen abziehen.
summary.loc["Spannweite"] = summary.loc["max"] - summary.loc["min"]
summary
| age | height | weight | nc.score | |
|---|---|---|---|---|
| min | 18.0 | 135.0 | 51.4 | 1.0 |
| max | 64.0 | 206.0 | 116.0 | 4.0 |
| Spannweite | 46.0 | 71.0 | 64.6 | 3.0 |
Die Spannweite hat wie der Mittelwert den Nachteil, dass sie durch Ausreißer beeinflusst wird. Daher ist die Spannweite kein gutes Streuungsmaß für einen Datensatz, der Ausreißer enthält. Ein weiterer Nachteil der Verwendung der Spannweite als Streuungsmaß ist, dass ihre Berechnung nur auf zwei Werten basiert: dem größten und dem kleinsten. Alle anderen Werte in einem Datensatz werden bei der Berechnung der Spanne ignoriert. Daher ist die Spannweite oftmals kein sehr zufriedenstellendes Maß für die Streuung ([Fahrmeir et al., 2016] s.62).
