Diskrete Zufallsvariablen und ihre Wahrscheinlichkeitsverteilungen
Contents
Diskrete Zufallsvariablen und ihre Wahrscheinlichkeitsverteilungen¶
import random
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
Eine Zufallsvariable ist eine Variable, deren Wert vom Zufall abhängt; dementsprechend ist ihr Wert mit einer Wahrscheinlichkeit verbunden. Generell sind Zufallsvariablen Zuordnungsvorschriften die möglichen Ergebnissen eines Zufallsexperiments einen Zahlenwert zuordnen. Eine diskrete Zufallsvariable weist den möglichen Ergebnissen diskrete, also abzählbare Werte zu. Eine Wahrscheinlichkeitsverteilung ist eine Auflistung der möglichen Werte und der entsprechenden Wahrscheinlichkeiten einer diskreten Zufallsvariablen, die häufig durch eine Formel dargestellt wird.
Ein Diagramm der Wahrscheinlichkeitsverteilung, das die Wahrscheinlichkeit jedes Wertes, dargestellt durch einen vertikalen Balken, dessen Höhe der Wahrscheinlichkeit entspricht, und die möglichen Werte einer diskreten Zufallsvariablen auf der horizontalen Achse anzeigt, wird Wahrscheinlichkeitshistogramm genannt.
Die Summe der Wahrscheinlichkeiten einer diskreten Zufallsvariablen für eine beliebige diskrete Zufallsvariable \(X\) wird geschrieben als
Bei einer großen Anzahl an voneinander unabhängigen Beobachtungen einer Zufallsvariablen \(X\) wird das Wahrscheinlichkeitshistogramm eine Annäherung an die Wahrscheinlichkeitsverteilung für \(X\) darstellen ([Fahrmeir et al., 2016] s.209-250).
Diskrete Zufallsvariablen - ein Beispiel¶
Lassen Sie uns das Konzept der diskreten Zufallsvariablen anhand eines Beispiels erläutern.
Unsere zu untersuchende Population besteht aus allen Studierenden, allen Dozenten und allen Verwaltungsmitarbeitern der FU Berlin. Wir wählen zufällig eine dieser Personen aus und fragen sie nach der Anzahl ihrer Geschwister. Folglich ist die Antwort, die Anzahl der Geschwister einer zufällig ausgewählten Person, eine diskrete Zufallsvariable, bezeichnet als \(X\). Der tatsächliche Wert (Anzahl der Geschwister) von \(X\) hängt vom Zufall ab, aber wir können trotzdem alle Werte von \(X\) auflisten, z.B. \(0\) Geschwister, \(1\) Geschwister, \(2\) Geschwister, usw. Zur Vereinfachung beschränken wir die Anzahl der Geschwister in dieser Übung auf \(5\).
Laut der Website der FU Berlin gibt es im WS 2021/2022 \(33.000\) Studierende, \(4.000\) Doktoranden, \(379\) Professoren und \(4.660\) Mitarbeiter an der FU Berlin (bitte beachten Sie, dass sich die tatsächlichen Zahlen im Laufe der Zeit ändern können).
Da wir keine Vorstellung von der damit verbundenen Wahrscheinlichkeit für eine bestimmte Anzahl von Geschwistern haben, starten wir einige Experimente:
Wir wählen eine zufällig ausgewählte Person aus und fragen nach der Anzahl der Geschwister.
Die Antwort lautet: \(0\)
Wir wählen zehn zufällig ausgewählte Personen aus und befragen sie zu ihren Geschwistern.
Die Antworten lauten: \(4,0,2,0,2,2,1,2,0,3\)
Wir wählen hundert Personen aus und fragen nach Geschwistern.
Die Antworten lauten: \(2, 0, 1, 2, 2, 0, 0, 0, 1, 3, 1, 2, 1, 0, 2, 0, 0, 2, 1, 1, 1, 1, 2, 2, 1, 2, 2, 0, 1, 1, 2, 4, 0, 3, 2, 0, 1, 2, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 2, 1, 1, 0, 2, 0, 1, 0, 1, 2, 1, 2, 1, 2, 2, 2, 1, 0, 2, 2, 4, 1, 2, 1, 1, 1, 1, 1, 0, 2, 1, 0, 1, 0, 1, 1, 2, 0, 2, 0, 0\)
Sie sehen, die Form der Notation wird ziemlich schnell unübersichtlich, wenn wir die Anzahl der abgefragten Individuen erhöhen. Wir beschließen also, die Häufigkeit und die entsprechende relative Häufigkeit der Werte für die Klassen \(0\), \(1\), \(2\), \(3\), \(4\), \(5\) (um es deutlich zu sagen: die letzte Klasse entspricht \(5\) oder mehr Geschwistern) zu notieren und das Experiment in Form einer schön formatierten Tabelle zu präsentieren.
Wir wählen \(1.000\) Personen aus und befragen sie zu ihren Geschwistern.
Geschwister (\(x\)) |
Absolute Häufigkeit(\(f\)) |
Relative Häufigkeit |
|---|---|---|
0 |
205 |
0,205 |
1 |
419 |
0,419 |
2 |
280 |
0,28 |
3 |
65 |
0,065 |
4 |
29 |
0,029 |
5 |
2 |
0,002 |
1000 |
1 |
Nachdem wir alle möglichen Werte aufgelistet und die entsprechenden relativen Häufigkeiten berechnet haben, kennen wir immer noch nicht genau die Wahrscheinlichkeiten der diskreten Zufallsvariablen \(X\) für die gesamte Population von \(40.961\) Personen, die der FU Berlin zugeordnet sind. Nach Gesprächen mit \(1.000\) zufällig ausgewählten Personen sind wir jedoch recht zuversichtlich, dass eine so große Anzahl von Interviews - verglichen mit der Anzahl der Gesamtpopulation \((40.961)\) - uns eine gute Annäherung an die Wahrscheinlichkeiten der diskreten Zufallsvariablen \(X\) (Anzahl der Geschwister) für die Gesamtpopulation liefern wird.
Im nächsten Schritt zeichnen wir ein Wahrscheinlichkeitshistogramm (der Stichprobe), das die möglichen Werte einer diskreten Zufallsvariablen \(X\) auf der horizontalen Achse und die Anteile dieser Werte auf der vertikalen Achse darstellt. Ein Verhältnishistogramm kann auch als Annäherung an die Wahrscheinlichkeitsverteilung dienen. Bitte beachten Sie, dass sowohl die Summe der Wahrscheinlichkeiten als auch die Summe der Anteile jeder diskreten Zufallsvariablen gleich \(1\) ist.
# Erzeuge Dataframe df
p = [0.205, 0.419, 0.28, 0.065, 0.029, 0.002]
x = [0, 1, 2, 3, 4, 5]
# Säulendiagramm
fig, ax = plt.subplots()
ax.bar(
x,
p,
width=1.0,
edgecolor="k",
)
# annotate
ax.bar_label(ax.containers[0], label_type="edge", size=12)
ax.set_title(
"Wahrscheinlichkeithistogramm der Zufallsvariablen X, die Anzahl der Geschwister zufällig \n ausgewählter Einzelpersonen der FU Berlin"
)
ax.set_xlabel("Anzahl Geschwister")
ax.set_ylabel("Wahrscheinlichkeit", color="k")
Text(0, 0.5, 'Wahrscheinlichkeit')
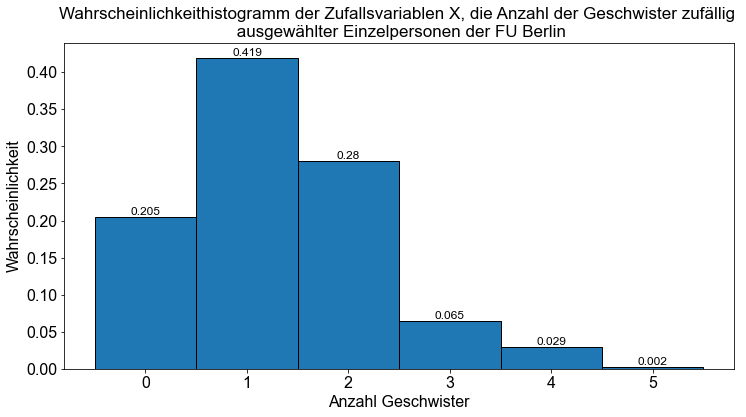
Bei vielen Anwendungen im wirklichen Leben kennen wir die Wahrscheinlichkeitsverteilung der Grundgesamtheit nicht - und werden sie auch nie kennen. Das liegt vor allem daran, dass in vielen Anwendungen die Grundgesamtheit viel zu groß ist oder es keine Möglichkeit gibt, zuverlässige Daten zu erhalten, oder wir weder das Geld noch die Zeit für eine umfassende Datenerhebung haben. Erhöht man jedoch die Anzahl der unabhängigen Beobachtungen einer Zufallsvariablen \(X\), so nähert sich das Wahrscheinlichkeitshistogramm der Stichprobe immer mehr dem Wahrscheinlichkeitshistogramm der Grundgesamtheit an. Um diese Behauptung zu beweisen, vergrößern wir unser Experiment:
Wir wählen nacheinander \(10\), \(100\) und \(1.000\) zufällig Personen aus, die mit der FU Berlin verbunden sind, und befragen sie nach der Anzahl der Geschwister. Wir werden jedes unserer drei Experimente aufzeichnen und schließlich mit der tatsächlichen/realen Wahrscheinlichkeitsverteilung vergleichen (Bitte beachten Sie, dass dieses Beispiel ein Übungsbeispiel ist und nicht die reale Anzahl der Geschwister in der Population der Personen an der FU Berlin darstellt; daher kennen die Dozenten des vorliegenden Skripts die Wahrscheinlichkeitsverteilung der Grundgesamtheit ;-))
_prob_experiment = (0.2, 0.425, 0.275, 0.07, 0.025, 0.005)
trialsize = [10, 100, 1000]
siblings = [0, 1, 2, 3, 4, 5]
np.random.seed(1)
fig, ax = plt.subplots(nrows=2, ncols=2, figsize=(14, 8))
ax = np.ravel(ax)
for e, n in enumerate(trialsize):
trial = np.random.choice(
range(len(_prob_experiment)), size=n, replace=True, p=_prob_experiment
)
unique_elements, counts_elements = np.unique(trial, return_counts=True)
counts = dict(zip(unique_elements, counts_elements / n))
df = pd.DataFrame.from_dict(counts, orient="index", columns=["frequency"])
df = df.reindex(siblings).fillna(0)
ax[e].bar(
df.index,
df.frequency,
width=1.0,
edgecolor="k",
)
ax[e].bar_label(ax[e].containers[0], label_type="edge", size=14)
ax[e].set_title(f"Häufigkeitsverteilung (n={n})")
ax[3].bar(
siblings,
_prob_experiment,
width=1.0,
edgecolor="k",
)
ax[3].bar_label(ax[3].containers[0], label_type="edge", size=14)
ax[3].set_title(f"Die tatsächliche (unbekannte) Häufigkeitsverteilung")
for _ax in ax:
_ax.set_ylim(0, 0.6)
_ax.set_xlabel("Anzahl Geschwister")
fig.tight_layout()
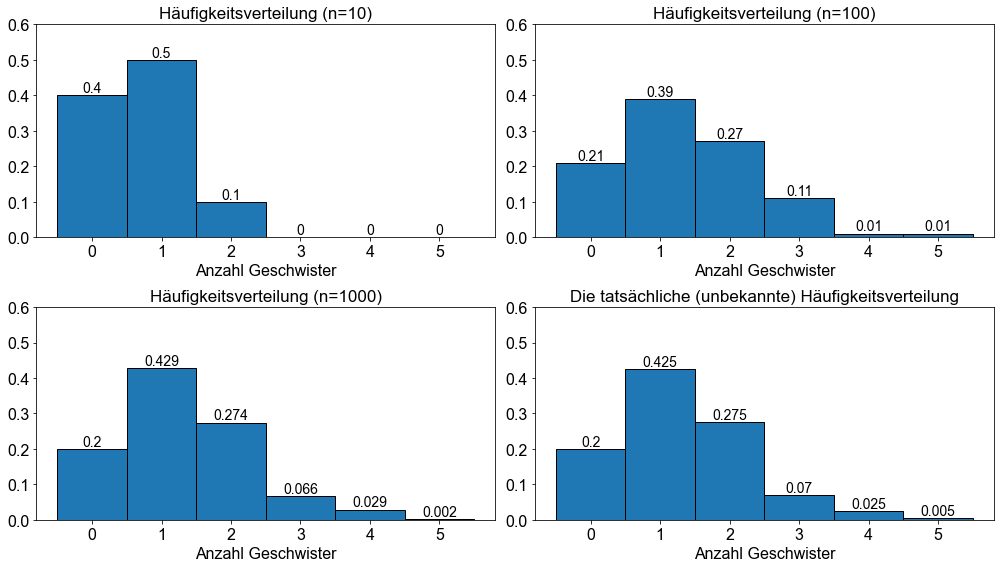
Die Diagramme bestätigen unsere Hypothese, dass sich das Histogramm der Stichprobe mit zunehmender Anzahl der Beobachtungen immer mehr dem Häufigkeitsverteilung der Grundgesamtheit annähert.
Der Mittelwert und die Standardabweichung einer diskreten Zufallsvariablen¶
Mittelwert einer diskreten Zufallsvariable¶
Der Mittelwert einer diskreten Zufallsvariablen \(X\) wird mit \(\mu_X\) oder, wenn keine Verwechslung auftreten soll, einfach mit \(\mu\) bezeichnet. Die Begriffe Erwartungswert, \(E(X)\) und Erwartung werden üblicherweise anstelle des Begriffs Mittelwert verwendet.
Bei einer großen Anzahl unabhängiger Beobachtungen einer Zufallsvariablen \(X\) nähert sich \(E(X)\) dieser Beobachtungen - der Stichprobe - dem Mittelwert \(\mu\) der Grundgesamtheit an. Je größer die Zahl der Beobachtungen ist, desto näher liegt \(E(X)\) an \(\mu\) ([Fahrmeir et al., 2016] s.226).
Erinnern wir uns an unser Experiment aus dem vorherigen Abschnitt, als wir \(1.000\) Personen ausgewählt und nach der Anzahl der Geschwister gefragt haben. Werfen wir noch einmal einen Blick auf die Tabelle, die das Experiment zusammenfasst
Geschwister (\(x\)) |
Absolute Häufigkeit(\(f\)) |
Relative Häufigkeit |
|---|---|---|
0 |
205 |
0,205 |
1 |
419 |
0,419 |
2 |
280 |
0,28 |
3 |
65 |
0,065 |
4 |
29 |
0,029 |
5 |
2 |
0,002 |
1000 |
1 |
Berechnen wir den Erwartungswert (Mittelwert) für dieses Experiment.
\(E(X) = \sum_{i=1}^{N}x_iP(X=x_i) \)
\( = 0 \cdot P(X=0) + 1 \cdot P(X=1)+ 2 \cdot P(X=2) + 3 \cdot P(X=3) +4 \cdot P(X=4)+ 5 \cdot P(X \ge 5) \)
\( = 0 \cdot 0,205 + 1 \cdot 0,419 + 2 \cdot 0,28+ 3 \cdot 0,065 + 4 \cdot 0,029 + 5 \cdot 0,002 \)
\( = 1,3 \)
Der sich daraus ergebende Erwartungswert von \(1,3\) liegt nahe am Mittelwert \(\mu\), den wir anhand der Wahrscheinlichkeiten der Grundgesamtheit berechnen (die realen Wahrscheinlichkeiten sind der unteren rechten Abbildung im vorherigen Abschnitt entnommen).
Übung¶
Betrachten wir einen fairen sechsseitigen Würfel. Wir können den Erwartungswert \(E(X)\) leicht mit Python berechnen. Der Begriff “fair” bedeutet, dass jede Zufallsvariable \(X=x_i,\; x \in 1,2,3,4,5,6\) mit gleicher Wahrscheinlichkeit auftritt. Daher ist \(P(X=x_i)=\frac{1}{6}\).
In Python schreiben wir den folgenden Code:
p_die = 1 / 6
die = pd.Series([1, 2, 3, 4, 5, 6])
die = die * p_die
sum(die)
3.5
Was aber, wenn wir uns nicht sicher sind, ob die Würfel wirklich fair sind? Woher wissen wir, dass wir nicht betrogen werden? Oder anders ausgedrückt: Wie oft müssen wir würfeln, bevor wir mehr Vertrauen haben können?
Führen wir ein Berechnungsexperiment durch: Wir wissen aus den obigen Überlegungen, dass der Erwartungswert eines \(6\)-seitigen fairen Würfels \(3,5\) ist. Wir führen ein Experiment durch, indem wir einen Würfel immer und immer wieder werfen. Wir speichern das Ergebnis und bevor wir erneut würfeln, berechnen wir den Durchschnitt aller bisherigen Würfelwürfe. Um dieses kleine Experiment durchzuführen, schreiben wir eine for-Schleife in Python.
# Setze random seed für Reproduzierbarkeit
random.seed(10)
wuerfel = []
e_wert = []
x = np.arange(0, 500, 1)
# Simuliere Würfelwurf
for i in range(500):
r = random.randint(1, 6)
wuerfel.append(r)
e_wert.append(np.mean(wuerfel))
# Plotten
fig, ax = plt.subplots()
ax.plot(x, e_wert, lw=1)
ax.axhline(y=3.5, color="C1", linestyle="dashed", label="Erwartungswert : 3,5")
ax.set_xlabel("Anzahl der Versuche")
ax.set_ylabel("Erwartungswert")
ax.set_ylim(1, 6.5)
ax.legend()
<matplotlib.legend.Legend at 0x166348040>
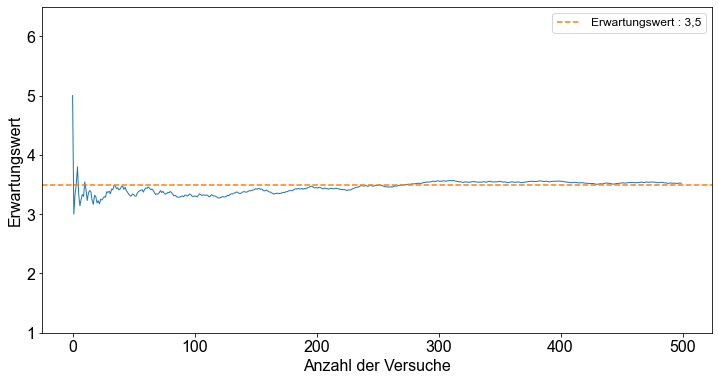
Das Diagramm zeigt, dass die Kurve nach anfänglichen Schwankungen schließlich abflacht und sich dem \(E(X)\) von \(3,5\) annähert.
Standardabweichung einer diskreten Zufallsvariable¶
Die Standardabweichung einer diskreten Zufallsvariablen \(X\) wird mit \(\sigma_X\) oder, wenn keine Verwechslung auftreten soll, einfach mit \(\sigma\) bezeichnet. Sie ist definiert als
