Varianzanalyse - ANOVA
Contents
Varianzanalyse - ANOVA¶
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import f, f_oneway, ttest_ind
import statsmodels.api as smi
from statsmodels.stats.multicomp import pairwise_tukeyhsd
In diesem Abschnitt wird eine Methode namens Varianzanalyse (englisch analysis of variance, kurz ANOVA) erörtert, mit der mehrere Mittelwerte einer Grundgesamtheit verglichen werden können.
Genauer gesagt geht es um die sogenannte einfaktorielle Varianzanalyse (Fahrmeir et al. [2016] s.478). Bei dieser Art der ANOVA werden die Mittelwerte einer Variablen verglichen, die sich aus der Klassifizierung durch eine andere Variable, dem sogenannten Faktor, ergeben. Um das Konzept zu veranschaulichen, wollen wir ein einfaches Beispiel entwerfen. Angenommen, wir vergleichen die mittleren Jahresgehälter der in Deutschland lebenden Personen, gruppiert nach Bundesländern, dann erhalten wir \(16\) Mittelwerte der Jahresgehälter, einen für jedes Bundesland. In diesem Beispiel ist die Bundeslandvariable also eine Klassifikationsvariable, der so genannte Faktor.
Bitte beachten Sie, dass die einfaktorielle Varianzanalyse die Verallgemeinerung des \(2\)-Stichproben \(t\)-Tests auf mehr als zwei Grundgesamtheiten ist.
Einfaktorielle ANOVA¶
Die grundlegende Logik einer einfaktoriellen ANOVA besteht darin, aus jeder Gruppe unabhängige Zufallsstichproben zu ziehen, dann die Stichprobenmittelwerte für jede Gruppe zu berechnen und anschließend die Variation der Stichprobenmittelwerte zwischen den Gruppen mit der Variation innerhalb der Gruppen zu vergleichen. Schließlich wird auf der Grundlage einer Teststatistik entschieden, ob die Mittelwerte der Gruppen gleich sind oder nicht.
Auf der Grundlage dieser Logik benötigen wir quantitative Maße für die Variabilität. Daher teilen wir die Gesamtvariabilität in zwei Segmente auf: Eines, das die Variabilität zwischen den Gruppen berücksichtigt, und das andere, das die Variabilität innerhalb der Gruppen berücksichtigt.
Maße der Variabilität¶
Wir führen drei quantitative Maße für die Variation ein:
Summe der Gesamtquadrate (SST)
Summe der Gruppenquadrate (SSG)
Summe der Fehlerquadrate (SSE)
Die Summe der Gesamtquadrate (SST) ist ein Maß für die Gesamtvariabilität der Variablen. Sie ist gegeben durch
wobei \(x_i\) den Beobachtungen in den Stichproben entspricht und \(\bar x\) für den Gesamtmittelwert aller Stichproben steht.
Die Summe der Gruppenquadrate (SSG) ist ein Maß für die Variabilität zwischen Gruppen und entspricht der quadrierten Abweichung der Gruppenmittelwerte vom Gesamtmittelwert, gewichtet mit dem Stichprobenumfang.
Dabei steht \(n_j\) für den Stichprobenumfang der Gruppe \(j\), \(\bar{x}_i\) für den Mittelwert der Gruppe \(j\) und \(\bar{x}\) für den Gesamtmittelwert der Stichprobe.
Die Summe der Fehlerquadrate (\(SSE\)) schließlich ist ein Maß für die Variabilität innerhalb der Gruppen. Sie steht im Zusammenhang mit der unerklärten Variabilität, d. h. der Variabilität, die nicht durch die Gruppenvariable erklärt werden kann. Die Summe der Fehlerquadrate ist gegeben durch
wobei \(n_j\) den Stichprobenumfang für Gruppe \(j\) und \(s^2_{j}\) die Varianz von Gruppe \(j\) bezeichnet. Alternativ kann man \(SSE\) sowie die Differenz von \(SST\) und \(SSG\) berechnen
Maße der mittleren Variabilität¶
Bisher haben wir Maße für die Gesamtvariabilität (\(SST\)), die Variabilität zwischen Gruppen (\(SSG\)) und die Variabilität innerhalb von Gruppen (\(SSE\)) berechnet. Um eine durchschnittliche Variabilität zu erhalten, skalieren wir im nächsten Schritt diese Variabilitätsmaße mit dem Stichprobenumfang (genauer gesagt mit den Freiheitsgraden, \(df\)).
Die Freiheitsgrade werden für jede Unterteilung der Variabilität (Gesamtvariabilität, Variabilität zwischen Gruppen und Variabilität innerhalb von Gruppen) definiert.
Gesamtvariabilität
wobei \(n\) den Gesamtumfang der Stichprobe bezeichnet. den Gesamtumfang der Stichprobe bezeichnet.
Variabilität zwischen den Gruppen
wobei \(k\) die Anzahl der Gruppen bezeichnet. den Gesamtumfang der Stichprobe bezeichnet.
Variabilität innerhalb der Gruppe
Nun können wir die mittleren Quadrate für die Variabilität zwischen den Gruppen und die Variabilität innerhalb der Gruppen berechnen. Die durchschnittliche Variabilität zwischen und innerhalb der Gruppen wird als die Gesamtvariabilität, skaliert mit den zugehörigen Freiheitsgraden, berechnet.
Mittlere Variabilität zwischen den Gruppen
Mittlere Variabilität innerhalb der Gruppe
Teststatistik und \(p\)-Wert¶
Schließlich vergleichen wir die mittlere Variation zwischen den Gruppen, \(MSG\), mit der Variation innerhalb der Gruppe, \(MSE\). Daher berechnen wir das Verhältnis zwischen der durchschnittlichen Variation zwischen den Gruppen (\(MSG\)) und der Variation innerhalb der Gruppen (\(MSE\)), das mit \(F\) bezeichnet wird.
Die \(F\)-Statistik hat die \(F\)-Verteilung (benannt nach Sir Ronald A. Fisher) mit
wobei \(k\) für die Anzahl der Gruppen und \(n\) für den Stichprobenumfang steht. Große Werte der \(F\)-Werte zeigen an, dass die Variation zwischen den Stichprobenmittelwerten der Gruppen im Verhältnis zur Variation innerhalb der Gruppe groß ist. Darüber hinaus können wir den \(p\)-Wert für jeden gegebenen \(F\)-Wert berechnen. Wenn der \(p\)-Wert klein ist, liefern die Daten überzeugende Beweise dafür, dass sich mindestens ein Paar von Gruppenmittelwerten voneinander unterscheidet. Ist der \(p\)-Wert groß, liefern die Daten keinen überzeugenden Beweis dafür, dass sich zumindest ein Paar von Gruppenmittelwerten voneinander unterscheidet, und die beobachteten Unterschiede in den Stichprobenmittelwerten sind somit auf Stichprobenvariabilität (oder Zufall) zurückzuführen.
Einfaktorielle ANOVA-Tabellen¶
Wie oben dargestellt, umfasst die einfache Varianzanalyse mehrere Analyseschritte. Dabei ist eine gängige Methode zur Darstellung einer einfachen ANOVA die so genannte einfaktorielle ANOVA-Tabelle. Der allgemeine Aufbau einer solchen Tabelle ist unten dargestellt.
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(k-1\) |
\(SSG\) |
\(MSG = \frac{SSG}{k-1}\) |
\(F=\frac{MSG}{MSE}\) |
\(p\) |
Fehler/Residuen |
\(n-k\) |
\(SSE\) |
\(MSE=\frac{SSE}{n-k}\) |
||
Insgesamt |
\(n-1\) |
\(SST\) |
Einfaktorieller ANOVA-Hypothesentest¶
Der Zweck eines einfaktoriellen ANOVA-Hypothesentests ist der Vergleich von \(k\) Grundgesamtheits-/Gruppenmittelwerten, \(\mu_1, \mu_2,...,\mu_k\). Die folgenden Annahmen müssen erfüllt sein, damit eine einseitige ANOVA angewendet werden kann (Fahrmeir et al. [2016] s.485):
Zufällige Stichproben
Unabhängige Stichproben
Für jede Grundgesamtheit ist die betrachtete Variable normalverteilt.
Die Standardabweichungen der betrachteten Variable sind für alle Grundgesamtheiten gleich.
Ein einfaktorieller ANOVA-Hypothesentest folgt demselben schrittweisen Verfahren wie andere Hypothesentests.
Schritt 1 |
Geben Sie die Nullhypothese \(H_0\) und alternative Hypothese \(H_A\) an |
Schritt 2 |
Legen Sie das Signifikanzniveau,\(\alpha\) fest |
Schritt 3 |
Berechnen Sie den Wert der Teststatistik |
Schritt 4 |
Bestimmen Sie den p-Wert |
Schritt 5 |
Wenn \(p \le \alpha\), \(H_0\) ablehnen; ansonsten \(H_0\) nicht ablehnen |
Schritt 6 |
Interpretieren Sie das Ergebnis des Hypothesentests |
Einfaktorieller ANOVA-Hypothesentest: Ein Beispiel¶
Um praktische Erfahrungen zu sammeln, wenden wir den einfaktoriellen ANOVA-Hypothesentest in einer Übung an. Dazu laden wir den students Datensatz. Sie können die Datei students.csv hier herunterladen. Importieren Sie den Datensatz und geben Sie ihm einen passenden Namen.
# Lese Datei students.csv als Dataframe ein
students = pd.read_csv("../../data/students.csv")
Der students Datensatz besteht aus \(8239\) Zeilen, von denen jede einen bestimmten Studenten repräsentiert, und \(16\) Spalten, von denen jede einer Variable/einem Merkmal entspricht, das sich auf diesen bestimmten Studenten bezieht. Diese selbsterklärenden Variablen sind: stud_id, name, gender, age, height, weight, religion, nc_score, semester, major, minor, score1, score2, online_tutorial, graduated, salary.
Um den einfaktoriellen ANOVA-Hypothesentest zu veranschaulichen, untersuchen wir das mittlere Jahresgehalt der Absolventen, gruppiert nach ihrem Hauptstudienfach. Zur Verdeutlichung: In diesem Beispiel erfolgt die Klassifizierung/Gruppierung durch eine Variable, die Hauptvariable, den so genannten Faktor, wir führen also eine einfaktorielle ANOVA durch. In dieser Übung wollen wir testen, ob sich das mittlere Jahresgehalt der Absolventen zwischen den Absolventen verschiedener Studienfächer unterscheidet.
Datenexploration und Aufbereitung¶
Wir beginnen unsere Datenanalyse mit dem Zufallsstichprobenverfahren. Wir ziehen eine Zufallsstichprobe von \(275\) Studenten aus dem Datensatz mit Hilfe der sample() Methode in Python. Wir wollen sicherstellen, dass wir nur Studenten mit abgeschlossenem Studium in die Stichprobe aufnehmen, deshalb unterteilen wir die Daten des Dataframes zuvor in Python. Des Weiteren reduzieren wir unseren Datensatz auf die zwei Variablen von Interesse, die kategoriale Variable major und die numerische Variable salary. Dann zeigen wir die ersten \(10\) Zeilen des Datensatzes an.
n = 275
data = students.loc[students["graduated"] == 1, ["major", "salary"]].sample(
n, random_state=1
)
data.head(10)
| major | salary | |
|---|---|---|
| 5019 | Biology | 49976.937146 |
| 4477 | Political Science | 27821.990115 |
| 241 | Environmental Sciences | 37668.890265 |
| 7166 | Biology | 60958.213489 |
| 2489 | Economics and Finance | 59920.480581 |
| 1194 | Mathematics and Statistics | 46116.221731 |
| 242 | Social Sciences | 35881.736200 |
| 2969 | Economics and Finance | 48456.787464 |
| 1476 | Mathematics and Statistics | 61384.549346 |
| 6765 | Biology | 61819.845923 |
Aus reinem Interesse visualisieren wir die Zählungen für jede der \(6\) verschiedenen Studienteilnehmer in unserer Stichprobe, indem wir ein Balkendiagramm erstellen. Wir verwenden die barh() Funktion aus der mathplotlib Bibliothek für die Darstellung.
fig, ax = plt.subplots()
data.groupby("major")["salary"].count().plot.barh(ax=ax)
ax.set_ylabel("")
ax.set_xlabel("Anzahl")
Text(0.5, 0, 'Anzahl')

Wir sehen, dass die verschiedenen Studienteilnehmer in unserer Stichprobe nicht gleich verteilt sind, aber das ist in Ordnung.
Bevor wir mit dem Hypothesentest beginnen, überprüfen wir, ob die Annahmen für den einfaktoriellen ANOVA-Hypothesentest erfüllt sind. Die Stichproben sind Zufallsstichproben und unabhängig. Das ist in Ordnung. Wir überprüfen die Normalitätsannahme, indem wir für jede gruppierte Variable ein Normalwahrscheinlichkeitsdiagramm (Q-Q-Diagramm) erstellen.
# Erzeuge Q-Q Plot
for _major in data.major.unique():
_ = smi.qqplot(data.loc[data["major"] == _major, "salary"], line="r")
ax = plt.gca()
ax.set_title(_major)
ax.set_xlabel("Theoretische Quantile")
ax.set_ylabel("Stichproben Quantile")
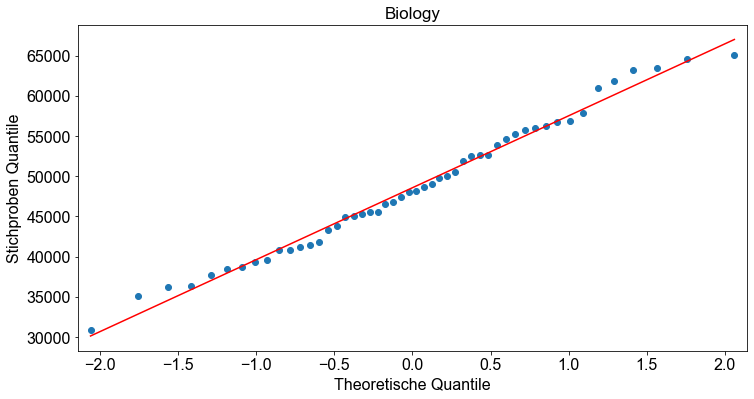
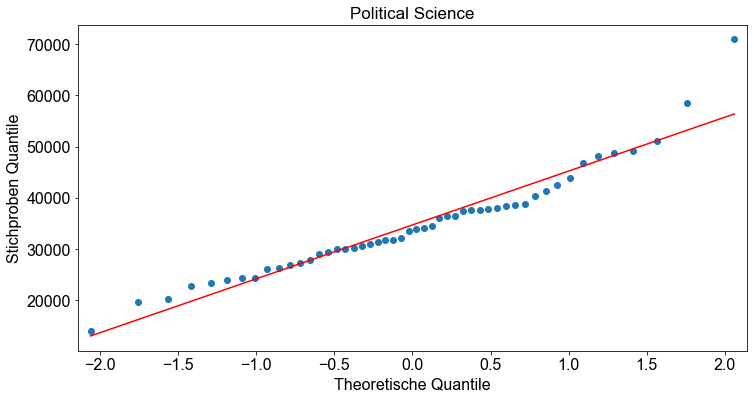
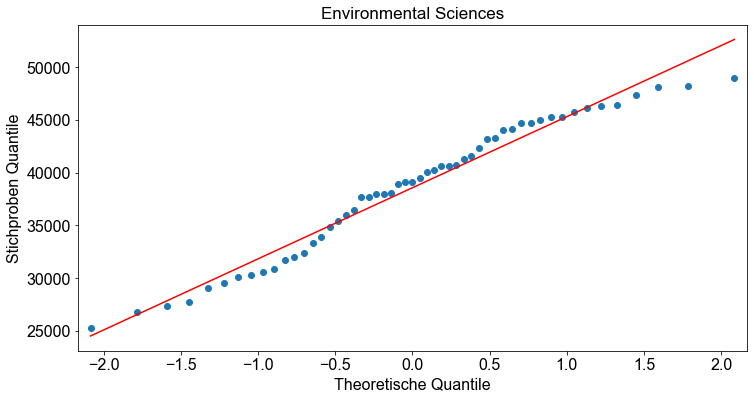
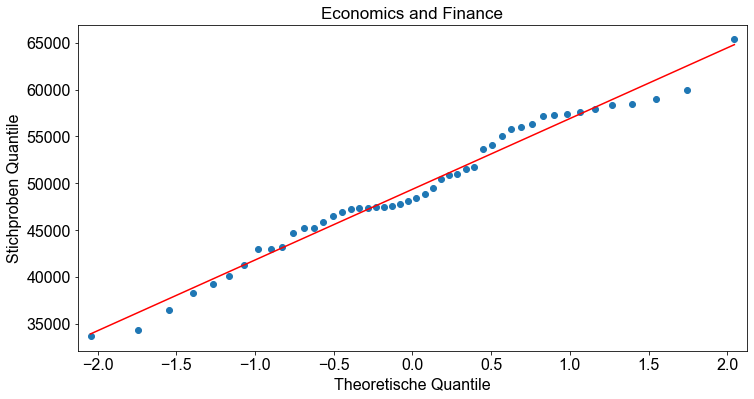
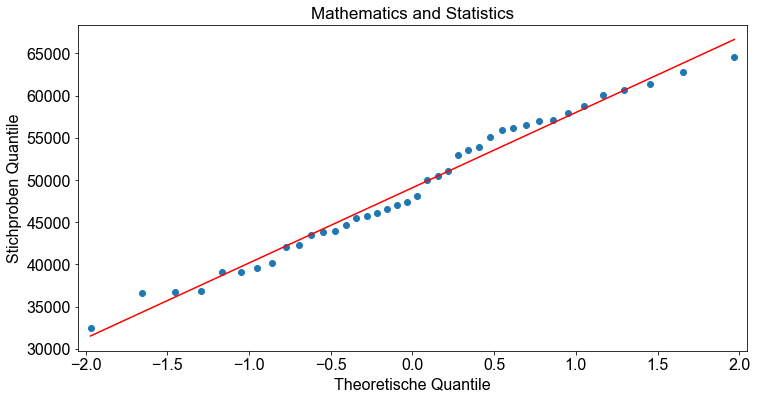
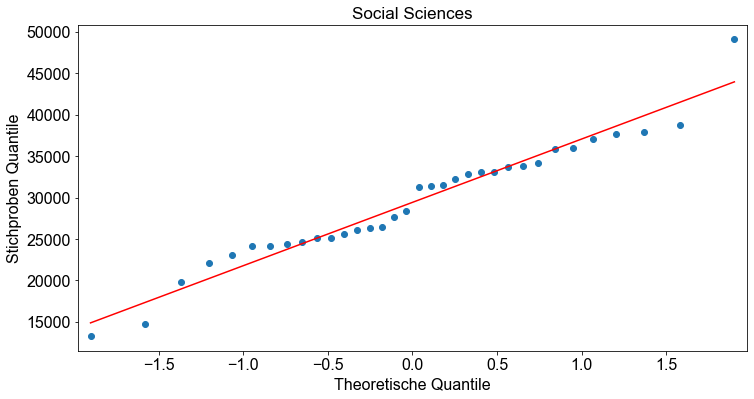
Als nächstes testen wir die Annahme gleicher Standardabweichungen. Dazu berechnen wir die Standardabweichung für jede Gruppe. Die Programmiersprache Python bietet einige ausgezeichnete Funktionen zur Berechnung statistischer Parameter für verschiedene Gruppierungen eines Datensatzes. Für unser Beispiel verwenden wir die Funktion pivot_table(), um die Standardabweichungen für jede Gruppe zu berechnen.
data.head()
| major | salary | |
|---|---|---|
| 5019 | Biology | 49976.937146 |
| 4477 | Political Science | 27821.990115 |
| 241 | Environmental Sciences | 37668.890265 |
| 7166 | Biology | 60958.213489 |
| 2489 | Economics and Finance | 59920.480581 |
table = data.groupby("major")["salary"].std()
table
major
Biology 8470.016077
Economics and Finance 7175.592532
Environmental Sciences 6460.464096
Mathematics and Statistics 8384.559216
Political Science 10273.903367
Social Sciences 7227.381892
Name: salary, dtype: float64
Als Faustregel gilt die Annahme gleicher Standardabweichungen als erfüllt, wenn das Verhältnis der größten zur kleinsten Standardabweichung der Stichprobe kleiner als \(2\) ist.
ratio = table.max() / table.min()
ratio
1.5902732705830243
Das Verhältnis zwischen der größten und der kleinsten Standardabweichung der Stichprobe beträgt \(1,59\). Das liegt nahe am Schwellenwert von \(2\), ist aber für unser Musterbeispiel noch akzeptabel. Daraus können wir schließen, dass die Annahmen erfüllt sind.
Beachten Sie, dass die einseitige ANOVA robust gegenüber moderaten Verstößen gegen die Normalitätsannahme und die Annahme gleicher Standardabweichungen ist (Fahrmeir et al. [2016] s.486).
Überprüfung der Hypothesen¶
Um den einfaktoriellen ANOVA-Hypothesentest durchzuführen, folgen wir dem schrittweisen Durchführungsverfahren für Hypothesentests.
Schritt 1 : Geben Sie die Nullhypothese \(H_0\) und alternative Hypothese \(H_A\) an
Die Nullhypothese besagt, dass das mittlere Jahresgehalt bei allen Gruppen von Absolventen gleich ist.
Alternative Hypothese
Schritt 2: Legen Sie das Signifikanzniveau,\(\alpha\) fest
alpha = 0.01
Schritt 3 und 4: Berechnen Sie den Wert der Teststatistik und den \(p\)-Wert
Um die \(F\)-Test-Statistik zu berechnen, müssen wir zuvor mehrere Größen bestimmen. Zur Veranschaulichung berechnen wir die \(F\)-Teststatistik manuell in Python. Schritt für Schritt füllen wir die ANOVA-Tabelle aus, bis wir schließlich die \(F\)-Teststatistik und folglich den \(p\)-Wert erhalten.
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(k-1\) |
\(SSG\) |
\(MSG = \frac{SSG}{k-1}\) |
\(F=\frac{MSG}{MSE}\) |
\(p\) |
Fehler/Residuen |
\(n-k\) |
\(SSE\) |
\(MSE=\frac{SSE}{n-k}\) |
||
Insgesamt |
\(n-1\) |
\(SST\) |
Wir beginnen mit der ersten Spalte und berechnen die Freiheitsgrade.
k = data["major"].nunique()
n = data.shape[0]
df_G = k - 1
df_G
5
df_E = n - k
df_E
269
df_T = n - 1
df_T
274
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(5\) |
\(SSG\) |
\(MSG = \frac{SSG}{k-1}\) |
\(F=\frac{MSG}{MSE}\) |
\(p\) |
Fehler/Residuen |
\(269\) |
\(SSE\) |
\(MSE=\frac{SSE}{n-k}\) |
||
Insgesamt |
\(274\) |
\(SST\) |
Außerdem berechnen wir die drei Summen der Quadrate, \(SST\), \(SSG\) und \(SSE\). Erinnern Sie sich an die Gleichungen von oben.
wobei \(x_i\)den Beobachtungen in den Stichproben und \(\bar x\) dem Gesamtmittelwert aller Stichproben entspricht.
# Berechne Gesamtmittelwert
x_bar = data["salary"].mean()
# Beobachtungen
xi = data["salary"]
# Berechne SST
SST = np.sum((xi - x_bar) ** 2)
SST
33169011167.80223
Dabei steht \(n_j\) für den Stichprobenumfang der Gruppe \(j, \bar{x}_i\) für den Mittelwert der Gruppe \(j\) und \(\bar x\) für den Gesamtmittelwert aller Stichproben.
n_j = data.groupby("major")["salary"].count()
n_j
major
Biology 50
Economics and Finance 48
Environmental Sciences 53
Mathematics and Statistics 40
Political Science 50
Social Sciences 34
Name: salary, dtype: int64
# Berechne Stichprobengrösse für alle Gruppen
n_j = data.groupby("major")["salary"].count()
# Berechne Mittelwert für alle Gruppen
xi_bar = data.groupby("major")["salary"].mean()
# Berechne SSG
SSG = np.sum(n_j * (xi_bar - x_bar) ** 2)
SSG
15425759144.907019
wobei \(n_j\) den Stichprobenumfang für die Gruppe \(j\) und \(s^2_j\) die Varianz der Gruppe \(j\) bezeichnet.
# Berechne Standardabweichung für die einzelnen Gruppen
s2_j = data.groupby("major")["salary"].std()
# Berechne SSE
SSE = np.sum((n_j - 1.0) * s2_j**2.0)
SSE
17743252022.895218
# alternativ kann SSE auch so berechnet werden
SSE2 = SST - SSG
SSE2
17743252022.89521
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(5\) |
\(1,542576 \cdot 10^{10}\) |
\(MSG = \frac{SSG}{k-1}\) |
\(F=\frac{MSG}{MSE}\) |
\(p\) |
Fehler/Residuen |
\(269\) |
\(1,774325 \cdot 10^{10}\) |
\(MSE=\frac{SSE}{n-k}\) |
||
Insgesamt |
\(274\) |
\(3,316901 \cdot 10^{10}\) |
Nun berechnen wir die beiden Maße für die mittlere Variabilität, \(MSG\) und \(MSE\).
# Berechne MSG
MSG = SSG / (k - 1)
MSG
3085151828.981404
# Berechne MSE
MSE = SSE / (n - k)
MSE
65960044.694777764
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(5\) |
\(1,542576 \cdot 10^{10}\) |
\(3,085152 \cdot 10^{9}\) |
\(F=\frac{MSG}{MSE}\) |
\(p\) |
Fehler/Residuen |
\(269\) |
\(1,774325 \cdot 10^{10}\) |
\(6,596004 \cdot 10^{7}\) |
||
Insgesamt |
\(274\) |
\(3,316901 \cdot 10^{10}\) |
Schließlich erhalten wir die \(F\)-Statistiken durch das Verhältnis von \(MSG\) und \(MSE\).
# Berechne Teststatistik
Fstat = MSG / MSE
Fstat
46.77304030428687
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(5\) |
\(1,542576 \cdot 10^{10}\) |
\(3,085152 \cdot 10^{9}\) |
\(46,77304\) |
\(p\) |
Fehler/Residuen |
\(269\) |
\(1,774325 \cdot 10^{10}\) |
\(6,596004 \cdot 10^{7}\) |
||
Insgesamt |
\(274\) |
\(3,316901 \cdot 10^{10}\) |
Im letzten Schritt berechnen wir den \(p\)-Wert durch Aufruf der Funktion f.cdf() in Python. Erinnern Sie sich, wie man die Freiheitsgrade berechnet.
Da die Nullhypothese nur dann abgelehnt wird, wenn die Teststatistik \(F\) zu groß ist, ist ein einfaktorieller ANOVA-Test immer rechtsschief.
df1 = k - 1
df2 = n - k
p_value = f.sf(Fstat, dfn=df1, dfd=df2)
p_value
1.0932120917246151e-34
Quelle |
\(df\) |
Summe der Quadrate (SS) |
Mittlere Quadrate (MS) |
\(F\)-Statistik |
\(p\)-Wert |
|---|---|---|---|---|---|
Gruppe/Klasse |
\(5\) |
\(1,542576 \cdot 10^{10}\) |
\(3,085152 \cdot 10^{9}\) |
\(46,77304\) |
\(1,093212 \cdot 10^{-34}\) |
Fehler/Residuen |
\(269\) |
\(1,774325 \cdot 10^{10}\) |
\(6,596004 \cdot 10^{7}\) |
||
Insgesamt |
\(274\) |
\(3,316901 \cdot 10^{10}\) |
Schritt 5: Wenn \(p \le \alpha , H_0\) ablehnen; ansonsten \(H_0\) nicht ablehnen
p_value <= alpha
True
Der \(p\)-Wert ist kleiner als das angegebene Signifikanzniveau von \(0,01\); wir verwerfen \(H_0\). Die Testergebnisse sind statistisch signifikant auf dem \(1 \%\)-Niveau und liefern einen sehr starken Beweis gegen die Nullhypothese.
Schritt 6: Interpretieren Sie das Ergebnis des Hypothesentests
\(p=1,093212 \cdot 10^{-34}\). Bei einem Signifikanzniveau von \(1 \%\) liefern die Daten sehr starke Hinweise darauf, dass sich mindestens ein Paar von Gruppenmittelwerten voneinander unterscheidet.
Hypothesentests in Python¶
Wir haben gerade einen einfaktoriellen ANOVA-Hypothesentest in Python manuell durchgeführt. Toll, aber jetzt wiederholen wir das Beispiel und nutzen die Möglichkeiten von Python, um das gleiche Ergebnis wie oben mit nur wenigen Zeilen Code zu erhalten!
Um einen einseitigen ANOVA-Hypothesentest in Python durchzuführen, verwenden wir die Funktion f_oneway(). Die f_oneway()-Funktion erwartet die Eingabe der zu vergleichenden Untergruppen. Hierfür verwenden wir eine list-comprehension. Außerdem lesen wir die \(F\)-Teststatistik statistics und \(p\)-Wert p_value aus.
dat = [
data.loc[data["major"] == major, "salary"].values
for major in data["major"].unique()
]
statistics, pvalue = f_oneway(*dat)
print(f"Wert der F-Statistik: {statistics}")
print(f"p-Wert: {pvalue}")
Wert der F-Statistik: 46.773040304286866
p-Wert: 1.0932120917246455e-34
Es hat gut funktioniert! Vergleichen Sie die Ausgabe der Funktion f_oneway() mit unserem Ergebnis von oben. Auch hier können wir zu dem Schluss kommen, dass die Daten bei einem Signifikanzniveau von \(1 \%\) sehr starke Hinweise darauf liefern, dass sich mindestens ein Paar von Gruppenmitteln voneinander unterscheidet.
Multiples Testproblem¶
Eine Einschränkung der ANOVA besteht darin, dass wir, wenn wir die Nullhypothese ablehnen, feststellen, dass die Mittelwerte der betrachteten Populationen nicht alle gleich sind. Wir können jedoch weder entscheiden, welche Mittelwerte unterschiedlich sind, noch, in welchem Verhältnis die Mittelwerte zueinander stehen.
Um diese Frage zu klären, wenden wir Methoden an, die als multiples Testen oder Mehrfachvergleiche bezeichnet werden. Das Problem bei Mehrfachvergleichen ist, dass je mehr Hypothesen für einen bestimmten Datensatz getestet werden, desto wahrscheinlicher ist es, dass die Nullhypothese fälschlicherweise zurückgewiesen wird. Daher erfordern die Methoden des Mehrfachvergleichs eine höhere Signifikanzschwelle (\(\alpha\)) für einzelne Vergleiche, um die Anzahl der gezogenen Schlüsse zu kompensieren.
Alphafehler-Kumulierung (engl. Family Wise Error Rate - FWER)¶
Eine Testfamilie ist der Fachbegriff für eine Reihe von Tests, die an einem Datensatz durchgeführt werden. Die Alphafehler-Kumulierung (engl. Family Wise Error Rate) ist die Wahrscheinlichkeit, dass bei der Durchführung von Mehrfachhypothesentests ein oder mehrere falsche Zurückweisungen der Null-Hypothese oder Fehler vom Typ I gemacht werden.
Es sei daran erinnert, dass bei einem Signifikanzniveau von \(\alpha=0,05\) die Wahrscheinlichkeit, einen Fehler vom Typ I zu machen, \(0,05\) oder \(5 \%\) beträgt. Folglich ist die Wahrscheinlichkeit, keinen Fehler vom Typ I zu machen, \(1-\alpha=1-0,05=0,95\). Außerdem ist die Wahrscheinlichkeit, zwei unabhängige Ereignisse zu beobachten, das Produkt ihrer Wahrscheinlichkeiten. Wenn wir also zwei unabhängige Tests durchführen, ist die Wahrscheinlichkeit, beim ersten und beim zweiten Test keinen Fehler vom Typ I zu machen
Wenn \(\alpha=0,05\) ist, ergibt sich eine Wahrscheinlichkeit, dass beim ersten und zweiten Test kein Fehler vom Typ I auftritt, von
Für eine Familie von \(C\)-Tests ist die Wahrscheinlichkeit, dass kein Fehler vom Typ I für die gesamte Familie auftritt, formal ausgedrückt
Betrachten wir nun \(C=10\) und \(\alpha=0,05\). Wir führen also \(10\) Mehrfachvergleiche mit einem Datensatz durch. Die Wahrscheinlichkeit, keinen Fehler vom Typ I in der Familie zu machen, ist dann
Folglich ist die Wahrscheinlichkeit, dass ein oder mehrere Fehler vom Typ I in der Testfamilie auftreten
Für unser Beispiel finden wir
Somit ist bei \(\alpha=0,05\) für jeden der \(10\) Mehrfachvergleiche die Wahrscheinlichkeit, dass die Nullhypothese falsch zurückgewiesen wird, \(0,401\) oder \(40,1 \%\).
Um diesem Problem Rechnung zu tragen, gibt es mehrere statistische Methoden. In diesem Abschnitt werden die Bonferroni-Korrektur und die Tukey-Test, auch bekannt als Tukeys HSD-Test (hoenstly significant difference), behandelt.
Beispiel-Daten¶
In diesem Abschnitt wiederholen wir das Beispiel aus dem vorherigen Abschnitt. Dort haben wir eine einfaktorielle ANOVA angewandt, um zu testen, ob sich das mittlere Jahresgehalt der Absolventen zwischen den Absolventen verschiedener Studienfächer unterscheidet. Dieses Mal werden wir jedoch mehrere Vergleiche durchführen, um die Beziehung zwischen allen Gruppenmittelwerten zu analysieren.
Laden Sie den students Datensatz erneut (Sie können die Datei students.csv hier herunterladen).
# Lese Datei students.csv als Dataframe ein
students = pd.read_csv("../../data/students.csv")
Der students Datensatz besteht aus \(8239\) Zeilen, von denen jede einen bestimmten Studenten repräsentiert, und \(16\) Spalten, von denen jede einer Variable/einem Merkmal entspricht, das sich auf diesen bestimmten Studenten bezieht. Diese selbsterklärenden Variablen sind: stud_id, name, gender, age, height, weight, religion, nc_score, semester, major, minor, score1, score2, online_tutorial, graduated, salary.
Aus dem Datensatz der Studierenden ziehen wir eine Zufallsstichprobe von \(275\) Absolventen und reduzieren den Datensatz auf die beiden interessierenden Variablen, die kategoriale Variable major und die numerische Variable salary. Für eine bessere Lesbarkeit in der folgenden Analyse ersetzen wir die Namen der Studienfächer durch entsprechende Abkürzungen.
n = 275
data = students.loc[students["graduated"] == 1, ["major", "salary"]].sample(
n, random_state=300
)
lookup = {
"Biology": "Bio",
"Political Science": "PoS",
"Economics and Finance": "EcFi",
"Environmental Sciences": "EnS",
"Mathematics and Statistics": "MaSt",
"Social Sciences": "SoS",
}
data["major"] = data["major"].apply(lambda x: lookup[x])
data.head(10)
| major | salary | |
|---|---|---|
| 3826 | MaSt | 57849.343490 |
| 795 | MaSt | 56558.160738 |
| 2127 | PoS | 46945.174104 |
| 1292 | Bio | 40093.455971 |
| 5913 | EnS | 35106.961865 |
| 1871 | EnS | 33216.118981 |
| 1853 | EnS | 30606.198317 |
| 1484 | PoS | 37240.113342 |
| 5619 | MaSt | 50913.038493 |
| 2299 | EcFi | 50365.098269 |
Des Weiteren führen wir einen einfaktoriellen ANOVA-Hypothesentest in Python durch, indem wir die Funktion f_oneway() anwenden.
dat = [
data.loc[data["major"] == major, "salary"].values
for major in data["major"].unique()
]
statistics, pvalue = f_oneway(*dat)
print(f"Wert der F-Statistik: {statistics}")
print(f"p-Wert: {pvalue}")
Wert der F-Statistik: 41.14261241723518
p-Wert: 2.283897894495435e-31
Bonferroni-Korrektur¶
Die Bonferroni-Korrektur kompensiert die erhöhte Wahrscheinlichkeit, dass eine Nullhypothese aufgrund von Mehrfachvergleichen fälschlicherweise abgelehnt wird (Fehler vom Typ I), indem das Signifikanzniveau \(\alpha\) in folgender Form angepasst wird
wobei \(m\) der Anzahl der Vergleiche entspricht, die gegeben ist durch
wobei \(k\) den Ebenen des Faktors entspricht, der die kategoriale Klassifikationsvariable ist.
def bonferroni(alpha, k):
"""Computes the boferroni correction"""
m = k * (k - 1) / 2
bonf = alpha / m
return bonf
Der paarweiser \(t\)-Test in Python: Bonferroni-Korrektur¶
Wie im vorigen Abschnitt erwähnt, ist eine einfaktorielle Varianzanalyse die Verallgemeinerung des \(2\)-Stichproben \(t\)-Tests auf mehr als zwei Grundgesamtheiten. Die Python-Funktion zur Durchführung von Mehrfachvergleichen ist ttest_ind(). Die Funktion ttest_ind() vergleicht die jeweiligen Gehaltsverteilungen (salary) nach Studienfächer gruppiert (major) miteinander.
Zunächst führen wir einen paarweisen \(t\)-Test ohne Anpassung durch, wodurch sich die Wahrscheinlichkeit erhöht, dass die Nullhypothese falsch zurückgewiesen wird.
from itertools import combinations
major = list(combinations(data.major.unique(), 2))
major
[('MaSt', 'PoS'),
('MaSt', 'Bio'),
('MaSt', 'EnS'),
('MaSt', 'EcFi'),
('MaSt', 'SoS'),
('PoS', 'Bio'),
('PoS', 'EnS'),
('PoS', 'EcFi'),
('PoS', 'SoS'),
('Bio', 'EnS'),
('Bio', 'EcFi'),
('Bio', 'SoS'),
('EnS', 'EcFi'),
('EnS', 'SoS'),
('EcFi', 'SoS')]
alpha = 0.05
for major1, major2 in major:
_, p_value = ttest_ind(
data.loc[data["major"] == major1, "salary"],
data.loc[data["major"] == major2, "salary"],
)
print(f"{major1} vs. {major2}")
print(f"p-value: {p_value}")
print(f"Reject H0 (p-value <= {alpha}): {p_value <= alpha}\n")
MaSt vs. PoS
p-value: 5.2857708581268477e-11
Reject H0 (p-value <= 0.05): True
MaSt vs. Bio
p-value: 0.23955813674375898
Reject H0 (p-value <= 0.05): False
MaSt vs. EnS
p-value: 2.8739133454494936e-10
Reject H0 (p-value <= 0.05): True
MaSt vs. EcFi
p-value: 0.6139629263411384
Reject H0 (p-value <= 0.05): False
MaSt vs. SoS
p-value: 1.0518783466253219e-10
Reject H0 (p-value <= 0.05): True
PoS vs. Bio
p-value: 4.8406849116995696e-15
Reject H0 (p-value <= 0.05): True
PoS vs. EnS
p-value: 0.120165093300726
Reject H0 (p-value <= 0.05): False
PoS vs. EcFi
p-value: 2.649042688427034e-12
Reject H0 (p-value <= 0.05): True
PoS vs. SoS
p-value: 0.23097741142110123
Reject H0 (p-value <= 0.05): False
Bio vs. EnS
p-value: 1.790220430001192e-14
Reject H0 (p-value <= 0.05): True
Bio vs. EcFi
p-value: 0.5127682352930607
Reject H0 (p-value <= 0.05): False
Bio vs. SoS
p-value: 6.474671293237731e-14
Reject H0 (p-value <= 0.05): True
EnS vs. EcFi
p-value: 8.151876693739742e-12
Reject H0 (p-value <= 0.05): True
EnS vs. SoS
p-value: 0.00557583127097583
Reject H0 (p-value <= 0.05): True
EcFi vs. SoS
p-value: 7.1456783247184506e-12
Reject H0 (p-value <= 0.05): True
Der paarweise \(t\)-Test zeigt, dass bei einem Signifikanzniveau von \(5 \%\) die Mittelwerte für \(5\) Kombinationen nicht statistisch signifikant unterschiedlich sind. Diese Kombinationen sind Bio-EcFi, Bio-MaSt, EcFi-MaSt, EnS-PoS, PoS-SoS mit \(p\)-Werten von \(0,5128\), \(0,2396\), \(0,61396\) , \(0,1202\) , \(0,635057\) bzw. \(0,230977\). Für die restlichen \(10\) Kombinationen verwerfen wir \(H_0\); d. h. für \(10\) Kombinationen sind die Mittelwerte bei einem Signifikanzniveau von \(5 \%\) unterschiedlich!
Zweitens führen wir einen paarweisen \(t\)-Test mit der Bonferroni-Anpassung durch.
bonf = bonferroni(alpha=0.05, k=data.major.nunique())
bonf
0.0033333333333333335
for major1, major2 in major:
_, p_value = ttest_ind(
data.loc[data["major"] == major1, "salary"],
data.loc[data["major"] == major2, "salary"],
)
print(f"{major1} vs. {major2}")
print(f"p-value: {p_value}")
print(f"Reject H0 (p-value <= {np.round(bonf,5)}): {p_value <= bonf}\n")
MaSt vs. PoS
p-value: 5.2857708581268477e-11
Reject H0 (p-value <= 0.00333): True
MaSt vs. Bio
p-value: 0.23955813674375898
Reject H0 (p-value <= 0.00333): False
MaSt vs. EnS
p-value: 2.8739133454494936e-10
Reject H0 (p-value <= 0.00333): True
MaSt vs. EcFi
p-value: 0.6139629263411384
Reject H0 (p-value <= 0.00333): False
MaSt vs. SoS
p-value: 1.0518783466253219e-10
Reject H0 (p-value <= 0.00333): True
PoS vs. Bio
p-value: 4.8406849116995696e-15
Reject H0 (p-value <= 0.00333): True
PoS vs. EnS
p-value: 0.120165093300726
Reject H0 (p-value <= 0.00333): False
PoS vs. EcFi
p-value: 2.649042688427034e-12
Reject H0 (p-value <= 0.00333): True
PoS vs. SoS
p-value: 0.23097741142110123
Reject H0 (p-value <= 0.00333): False
Bio vs. EnS
p-value: 1.790220430001192e-14
Reject H0 (p-value <= 0.00333): True
Bio vs. EcFi
p-value: 0.5127682352930607
Reject H0 (p-value <= 0.00333): False
Bio vs. SoS
p-value: 6.474671293237731e-14
Reject H0 (p-value <= 0.00333): True
EnS vs. EcFi
p-value: 8.151876693739742e-12
Reject H0 (p-value <= 0.00333): True
EnS vs. SoS
p-value: 0.00557583127097583
Reject H0 (p-value <= 0.00333): False
EcFi vs. SoS
p-value: 7.1456783247184506e-12
Reject H0 (p-value <= 0.00333): True
Der paarweise \(t\)-Test mit der Bonferroni-Anpassung zeigt, dass bei einem Signifikanzniveau von \(5 \%\) die Mittelwerte für \(6\) Kombinationen nicht statistisch signifikant unterschiedlich sind. Bei diesen Kombinationen handelt es sich um Bio-EcFi, Bio-MaSt, EcFi-MaSt, EnS-PoS, PoS-SoS, EnS-SoS mit \(p\)-Werten von \(0,5128\), \(0,2396\), \(0,61397\), \(0,1202\), \(0,230978\) bzw. \(0,00558\). (beim Bonferroni-Verfahren wird \(\alpha\) durch die Anzahl der Tests geteilt bzw. der \(p\)-Wert mit dieser Anzahl multipliziert und auf \(1\) gekürzt, wenn das Ergebnis über \(1\) liegt und somit keine Wahrscheinlichkeit darstellt). Für die verbleibenden \(9\) Kombinationen haben wir \(H_0\) abgelehnt, d. h. für \(9\) Kombinationen sind die Mittelwerte bei einem Signifikanzniveau von \(\approx 0,0067 \%\) unterschiedlich!
Tukey-Mehrfach-Vergleichsmethode¶
Der Tukey-Test, auch bekannt als Tukey’s HSD-Test (honest significant difference), basiert auf der studentized range-Verteilung, die manchmal auch als \(q\)-Verteilung bezeichnet wird. Die \(q\)-Verteilung ist eine rechtsschiefe Wahrscheinlichkeitsdichtekurve mit zwei Parametern, \(\kappa\) und \(\nu\), die ihre Form beschreiben. Diese Parameter sind gegeben durch
und
wobei \(n\) die Gesamtzahl der Beobachtungen ist und \(k\) die Anzahl der Gruppen/Klassen.
Der Tukey-Test vergleicht die Mittelwerte jeder Gruppe mit den Mittelwerten jeder anderen Gruppe. Er liefert das Konfidenzintervall für jedes
Wenn das Konfidenzintervall für einen paarweisen Vergleich \(0\) einschließt, wird \(H_0\) nicht verworfen, es wird nicht angenommen, dass sie signifikant unterschiedlich sind. Alle anderen Paare, für die das Konfidenzintervall nicht \(0\) einschließt, sind signifikant unterschiedlich, \(H_0\) wird also verworfen.
Tukey’s Test in Python¶
In Python werden Tukey’s HSD Tests durch die pairwise_tukeyhsd() Funktion berechnet. Die pairwise_tukeyhsd()-Funktion erwartet als Eingabe endog, die zu vergleichende Größe und groups die Aufteilung der Gruppen. Um die Breite der Konfidenzintervalle festzulegen, geben wir der Funktion das Konfidenzniveau mit dem Argument alpha an.
# Tukey's test ausführen
tukey = pairwise_tukeyhsd(endog=data["salary"], groups=data["major"], alpha=0.05)
tukey.summary()
| group1 | group2 | meandiff | p-adj | lower | upper | reject |
|---|---|---|---|---|---|---|
| Bio | EcFi | -1012.3086 | 0.983 | -5228.585 | 3203.9678 | False |
| Bio | EnS | -11777.6601 | -0.0 | -15810.772 | -7744.5482 | True |
| Bio | MaSt | -1846.3679 | 0.8039 | -6036.7581 | 2344.0223 | False |
| Bio | PoS | -13913.133 | -0.0 | -18078.5879 | -9747.6782 | True |
| Bio | SoS | -16091.4853 | -0.0 | -21100.7005 | -11082.2702 | True |
| EcFi | EnS | -10765.3515 | 0.0 | -15067.6403 | -6463.0628 | True |
| EcFi | MaSt | -834.0593 | 0.9946 | -5284.1231 | 3616.0045 | False |
| EcFi | PoS | -12900.8245 | -0.0 | -17327.4159 | -8474.233 | True |
| EcFi | SoS | -15079.1768 | -0.0 | -20307.5545 | -9850.799 | True |
| EnS | MaSt | 9931.2922 | 0.0 | 5654.369 | 14208.2155 | True |
| EnS | PoS | -2135.4729 | 0.7016 | -6387.9683 | 2117.0224 | False |
| EnS | SoS | -4313.8252 | 0.1475 | -9395.6496 | 767.9991 | False |
| MaSt | PoS | -12066.7651 | 0.0 | -16468.7074 | -7664.8229 | True |
| MaSt | SoS | -14245.1174 | 0.0 | -19452.6425 | -9037.5924 | True |
| PoS | SoS | -2178.3523 | 0.834 | -7365.8335 | 3009.1289 | False |
Bitte beachten Sie, dass wir im Fall ohne \(p\)-Wert-Anpassung die Nullhypothese für \(10\) Kombinationen abgelehnt haben. Beim paarweisen \(t\)-Test mit der Tukey-Anpassung wurde die Nullhypothese für \(9\) Kombinationen verworfen.
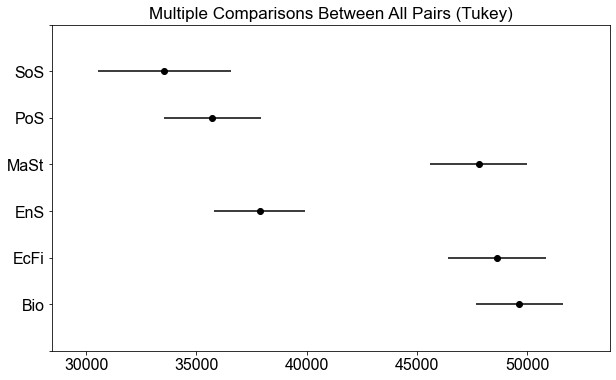
Die Tabelle zeigt die Differenz zwischen den einzelnen Paaren, die \(95 \%\)-Konfidenzintervalle und den \(p\)-Wert der paarweisen Vergleiche. Schauen Sie sich die Tabelle genau an, und Sie werden sehen, dass für alle \(6\) Vergleiche, bei denen das Konfidenzintervall \(0\) einschließt, der \(p\)-Wert höher ist als das Signifikanzniveau \(\alpha\). Wenn \(p \gt \alpha\) ist, verwerfen wir \(H_0\) nicht, d. h. es gibt keinen statistisch signifikanten Unterschied zwischen den Mittelwerten dieser beiden Gruppen. Für alle Paare, bei denen \(p \le \alpha\) ist, verwerfen wir dagegen \(H_0\) und stellen fest, dass ein statistisch signifikanter Unterschied zwischen den Mittelwerten dieser Paare besteht. Die tukey.plot_simultaneous()-Funktion bietet eine nette Plot-Funktion, die die Konfidenzintervalle für jedes Paar visualisiert.
_ = tukey.plot_simultaneous()