Die Poisson-Verteilung
Contents
Die Poisson-Verteilung¶
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import poisson
Eine weitere wichtige diskrete Wahrscheinlichkeitsverteilung ist die Poisson-Verteilung, benannt zu Ehren des französischen Mathematikers und Physikers Simeon D. Poisson (1781-1840). Die Poisson-Verteilung wird häufig verwendet, um die Wahrscheinlichkeit zu beschreiben, dass eine Reihe von Ereignissen in einem bestimmten Zeit- oder Raumintervall eintritt, wobei die Wahrscheinlichkeit des Auftretens dieser Ereignisse sehr gering ist (Papula [2016] s.367). Da die Anzahl der Versuche jedoch sehr groß ist, treten diese Ereignisse tatsächlich ein.
Die Zufallsvariable \(X\), die als Poisson-Zufallsvariable bezeichnet wird, ist die Anzahl der Ereignisse (oder des Eintreffens) solcher Ereignisse in einem bestimmten Zeit- oder Raumintervall. Eine Poisson-Zufallsvariable hat unendlich viele mögliche Werte, nämlich alle ganzen Zahlen (Fahrmeir et al. [2016] s.242).
Unter der Annahme, dass \(\lambda\) der Erwartungswert solcher Ankünfte in einem Zeitintervall fester Länge ist, ist die Wahrscheinlichkeit, genau \(x\) Ereignisse zu beobachten, durch die Wahrscheinlichkeitsfunktion gegeben
wobei \(\lambda\) eine positive reelle Zahl ist, die die durchschnittliche Anzahl der Ereignisse während eines festen Zeitintervalls darstellt, und \(e≈2,7182818\) (die Eulersche Zahl). Somit wird jede bestimmte Poisson-Verteilung durch einen Parameter identifiziert, der gewöhnlich mit \(\lambda\) (dem griechischen Buchstaben Lambda) bezeichnet wird. Wenn das Ereignis beispielsweise durchschnittlich \(10\) Mal pro Sekunde auftritt, tritt es in \(60\) Sekunden durchschnittlich \(600\) Mal auf und \(\lambda=600\).
Die Poisson-Verteilung - ein Beispiel¶
Wenden wir die Poisson-Verteilung in Form eines Beispiels an. Wir konzentrieren uns auf das Jahrhunderthochwasser, ein Konzept, das im Flussbau häufig zur Planung von Hochwasserschutzmaßnahmen verwendet wird.
Erinnern wir uns an die mathematische Notation einer Poisson-Zufallsvariablen:
wobei \(\lambda\) eine positive reelle Zahl ist, die die durchschnittliche Anzahl der Ereignisse während eines festen Zeitintervalls darstellt, und \(e≈2,7182818\).
Das Jahrhunderthochwasser ist eine Kurzbezeichnung für ein Hochwasser mit einer jährlichen Überschreitungswahrscheinlichkeit von \(1 \%\) und einem durchschnittlichen Wiederholungsintervall von \(100\) Jahren. Der Begriff kann jedoch für Menschen irreführend sein, denn sie stellen sich vor, dass der Begriff Hochwasser beschreibt, die einmal alle \(100\) Jahre auftreten. Dies ist jedoch nicht der Fall. Ein Hochwasser mit einer jährlichen Überschreitungswahrscheinlichkeit von \(1 \%\) bedeutet, dass in jedem einzelnen Jahr mit einer Wahrscheinlichkeit von \(0,01\) ein Hochwasser in einer Größenordnung auftritt, die einem Jahrhunderthochwasser entspricht.
Im Rahmen einer Poisson-Verteilung wird der Erwartungswert \(E(x)=\lambda\) eines solchen Hochwassers während des festen Intervalls von \(100\) Jahren auf \(\lambda=100×0,01=1\) gesetzt. Die Poisson-Zufallsvariable \(X\) ist also die Anzahl der Ereignisse, die natürlich je nach Fragestellung verschiedene Werte annehmen kann. Wir können uns für die Wahrscheinlichkeit interessieren, dass ein solches Hochwasserereignis während des \(100\)-Jahres-Intervalls nicht auftritt, \(P(x=0)\), oder wir wollen die Wahrscheinlichkeit wissen, dass ein solches Hochwasserereignis genau einmal während des \(100\)-Jahres-Intervalls auftritt, also \(P(x=1)\), oder wir wollen die Wahrscheinlichkeit wissen, dass zwei oder mehr solcher Hochwasserereignisse während des \(100\)-Jahres-Intervalls auftreten, also \(P(x≥2)\). Setzt man diese Werte in die obige Gleichung ein, so erhält man
\(\lambda = 1, x = 0,1,2,\dots ,n\)
Wir wenden uns an Python, um die Berechnungen durchzuführen. Wir werden die Funktionen poisson.pmf und poisson.cdf verwenden.
x_0 = poisson.pmf(0, mu=1)
x_0
0.36787944117144233
x_1 = poisson.pmf(1, mu=1)
x_1
0.36787944117144233
xge2 = 1 - x_1 - x_0
xge2
0.26424111765711533
Alternativ können wir doe poisson.cdf verwenden.
1 - poisson.cdf(1, mu=1)
0.26424111765711533
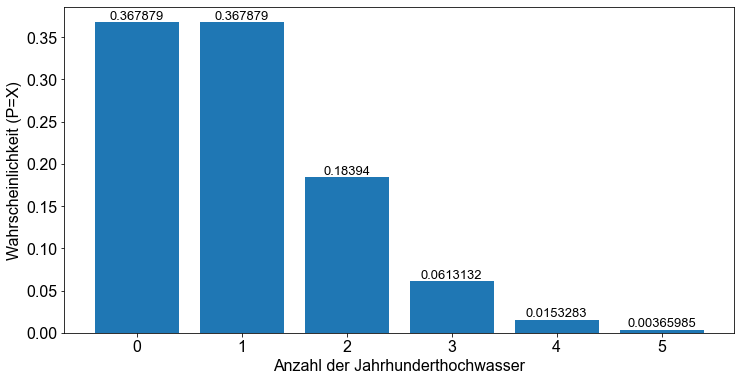
Die Ergebnisse zeigen, dass die Wahrscheinlichkeit, dass während eines Zeitraums von \(100\) Jahren kein Hochwasser \(P(X=0)\) in einer Größenordnung auftritt, die einem Jahrhunderthochwasser entspricht, \(0,37 \) beträgt, was interessanterweise genauso wahrscheinlich ist wie das Auftreten von genau einem Hochwasser \(P(X=1)\). Die Wahrscheinlichkeit, dass zwei oder mehr \(P(X≥2)\) solcher Hochwasserereignisse innerhalb des \(100\)-Jahres-Intervalls auftreten, ist \(0,26\) und damit geringer. Beachten Sie jedoch, dass die Wahrscheinlichkeit, dass zwei oder mehr \(P(X≥2)\) solcher Hochwasserereignisse während des 100-Jahres-Intervalls eintreten, etwa \(26 \%\) beträgt!
Zur Überprüfung der Richtigkeit addieren wir die Wahrscheinlichkeiten \(P(x=0), P(x=1)\) und \(P(x≥2)\), was \(1\) ergeben sollte,
x_0 + x_1 + xge2
1.0
Zur besseren Veranschaulichung stellen wir die Wahrscheinlichkeiten der Poisson-Zufallsvariablen \(x=0,1,2,3,4,≥5\) dar.
xs = [0, 1, 2, 3, 4, 5]
res = []
for x in xs:
if x != 5:
p = poisson.pmf(x, mu=1)
else:
p = 1 - poisson.cdf(4, mu=1)
res.append(p)
fig, ax = plt.subplots()
ax.bar(xs, height=res)
_ = ax.bar_label(ax.containers[0], label_type="edge", size=13)
ax.set_xlabel("Anzahl der Jahrhunderthochwasser")
ax.set_ylabel("Wahrscheinlichkeit (P=X)")
Text(0, 0.5, 'Wahrscheinlichkeit (P=X)')
Form, Mittelwert und Standardabweichung einer Poisson-Verteilung¶
Alle Poisson-Verteilungen sind rechtsschief. Der Mittelwert \(\mu\) und die Standardabweichung \(\sigma\) einer Poisson-Zufallsvariablen mit dem Parameter \(\lambda\) sind
und
Poisson-Approximation an die Binomialverteilung¶
In Situationen, in denen \(n\) groß und \(p\) sehr klein ist, kann die Poisson-Verteilung zur Annäherung an die Binomialverteilung verwendet werden. Erinnern Sie sich an die binomische Wahrscheinlichkeitsverteilung:
Wie im früheren Beispiel “Jahrhunderthochwasser” ist \(n\) eine große Zahl \((100)\) und \(p\) eine kleine Zahl \((0,01)\). Einsetzen in die Gleichung von oben \(P(x=1)\) ergibt
\( P(X = 1) = {100 \choose 1}\times 0,01^1\times (1 - 0,01)^{100 -1} \)
\( = 100\times 0,01\times 0,3697296 \)
\( = 0,3697296 \)
Das Ergebnis kommt dem oben ermittelten Ergebnis sehr nahe poisson.pmf(1,1) \(= 0,3678794\). Die geeignete Poisson-Verteilung ist diejenige, deren Mittelwert gleich dem der Binomialverteilung ist, d. h. \(\lambda=np\), was in unserem Beispiel \(\lambda=100×0,01=1\) ist.
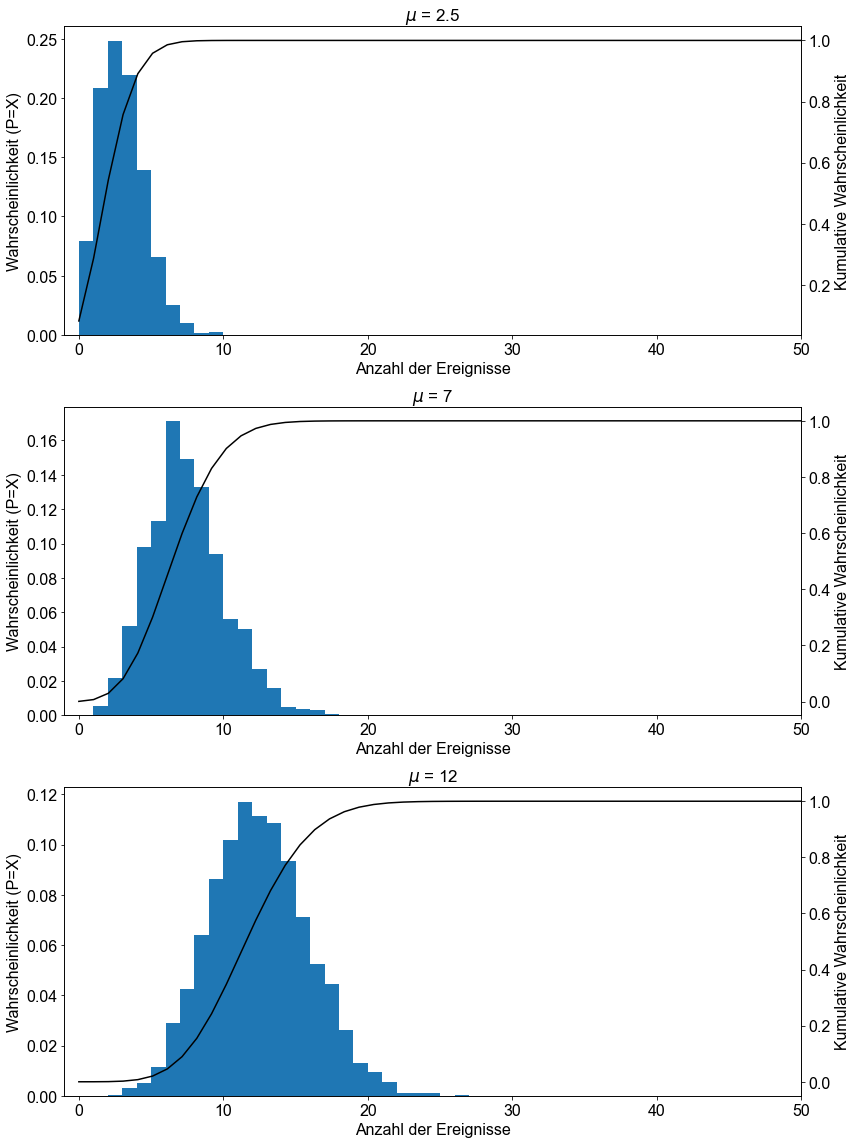
Zum Abschluss dieses Abschnitts und um Ihnen eine Vorstellung von den Formen der verschiedenen Poisson-Wahrscheinlichkeitsverteilungen zu geben, werden im Folgenden drei verschiedene Poisson-Wahrscheinlichkeitsverteilungen und die entsprechenden kumulativen Poisson-Wahrscheinlichkeitsverteilungen für \(\lambda=2,5, \lambda=7\) und \(\lambda=12\) angegeben.
lambdas = [2.5, 7, 12]
fig, ax = plt.subplots(nrows=len(lambdas), figsize=(12, 16))
for e, _lambda in enumerate(lambdas):
x = poisson.rvs(_lambda, size=2000)
bins = max(x) - min(x)
ax[e].hist(x, bins, density=True)
ax[e].set_xlabel("Anzahl der Ereignisse")
ax[e].set_ylabel("Wahrscheinlichkeit (P=X)")
ax[e].set_title(f"$\mu$ = {_lambda}")
x = np.linspace(0, 50, 50)
cdf = poisson.cdf(x, mu=_lambda)
ax2 = ax[e].twinx()
ax2.set_ylabel("Kumulative Wahrscheinlichkeit")
ax2.plot(x, cdf, color="k")
ax[e].set_xlim(-1, 50)
fig.tight_layout()