Contents

Inferenz für die Standardabweichung der Grundgesamtheit

Inferenz für die Standardabweichung der Grundgesamtheit

Bisher haben wir Methoden der Inferenzstatistik erörtert, die sich auf Aussagen über einen oder mehrere Grundgesamtheitsmittelwerte konzentrieren. In den folgenden Abschnitten betrachten wir Methoden der Inferenzstatistik, die Aussagen über die Varianzen (oder Standardabweichungen) der Grundgesamtheit liefern. Wir erinnern daran, dass die Varianz (\(\sigma^2\)) und die Standardabweichung (\(\sigma\)) ein Maß für die Streuung und Variabilität einer Variablen sind.

Inferenz für die Standardabweichung einer Grundgesamtheit

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from random import sample
import statsmodels.api as smi

Inferenz für eine Grundgesamtheitsstandardabweichung basiert auf der Chi-Quadrat (\(\chi^2\))-Verteilung. Eine \(\chi^2\)-Verteilung ist eine rechtsschiefe Wahrscheinlichkeitsdichtekurve. Die Form der \(\chi^2\)-Kurve wird durch ihre Freiheitsgrade (\(df\)) bestimmt.

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

df = [1, 2, 3, 5, 7, 10]

x = np.linspace(0, 14, 1000)
fig, ax = plt.subplots()
for _df in df:
    ax.plot(x, chi2.pdf(x, df=_df), label=f"df={_df}")
ax.set_title(
    "$\chi^2$-Warscheinlichkeitsdichtefunktion mit unterschiedlichen Freiheitsgraden (df)"
)
ax.legend(fontsize=18)
ax.set_ylim(-0.02, 0.5)
ax.axvline(0, color="k")

<matplotlib.lines.Line2D at 0x16d79c8b0>
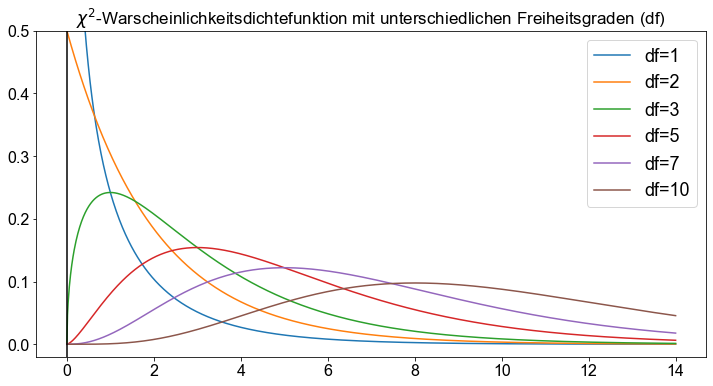
../_images/04_Standardabweichung_der_Grundgesamtheit_6_1.png

Um einen Hypothesentest für eine Populationsstandardabweichung durchzuführen, wird ein \(\chi^2\)-Wert mit einer bestimmten Fläche unter einer \(\chi^2\)-Kurve in Beziehung gesetzt. Entweder wir ziehen eine \(\chi^2\)-Tabelle, um diesen Wert nachzuschlagen, oder wir machen von der Python-Maschinerie Gebrauch.

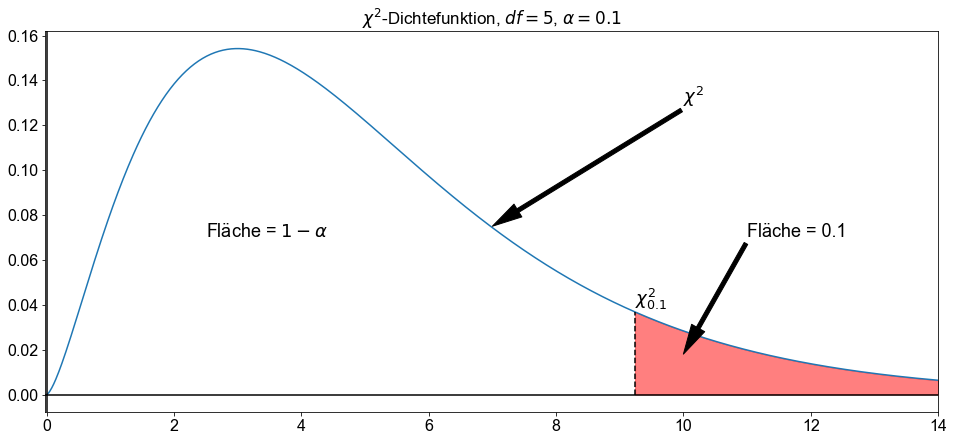
Bei gegebenen \(\alpha\), wobei \(\alpha\) einer Wahrscheinlichkeit zwischen \(0\) und \(1\) entspricht, bezeichnet \(\chi^2_\alpha\) den \(\chi^2\) -Wert, der die Fläche \(\alpha\) zu seiner Rechten unter einer \(\chi^2\) -Kurve hat.

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

df = 5
alpha = 0.9
x = np.linspace(0, 16, 1000)
fig, ax = plt.subplots(figsize=(16, 7))
ax.plot(x, chi2.pdf(x, df=df))
ax.set_xlim(-0.02, 14)
ax.axvline(0, color="k")
ax.axhline(0, color="k")
ax.vlines(
    chi2.ppf(alpha, df=df),
    ymin=0,
    ymax=chi2.pdf(chi2.ppf(alpha, df=df), df=df),
    color="k",
    linestyle="dashed",
)

ax.fill_between(
    x, chi2.pdf(x, df=df), where=x >= chi2.ppf(alpha, df=df), color="r", alpha=0.5
)

ax.set_title(r"$\chi^2$-Dichtefunktion, $df=5$, $\alpha=0.1$")


ax.annotate(
    r"$\chi^2$",
    xy=(7, 0.075),
    xytext=(10, 0.13),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=18,
)

ax.annotate(
    r"Fläche = 0.1",
    xy=(10, 0.018),
    xytext=(11, 0.07),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=18,
)

ax.text(s="$\chi^2_{0.1}$", x=chi2.ppf(alpha, df=df), y=0.04, size=18)
ax.text(s=r"Fläche = $1 - \alpha$", x=2.5, y=0.07, size=18)

Text(2.5, 0.07, 'Fläche = $1 - \\alpha$')
../_images/04_Standardabweichung_der_Grundgesamtheit_8_1.png

Intervall-Schätzung von \(\sigma\)

Das \(100(1-\alpha)\%\)-Konfidenzintervall für \(\sigma\) beträgt

\[\sqrt{\frac{n-1}{\chi^2_{\alpha/2}}} \le \sigma \le \sqrt{\frac{n-1}{\chi^2_{1-\alpha/2}} }\]

\(\chi^2\)-Test auf Standardabweichung

Das Hypothesentestverfahren für eine Standardabweichung wird als \(\chi^2\)-Test auf Standardabweichung bezeichnet. Hypothesentests für Varianzen folgen demselben schrittweisen Verfahren wie Hypothesentests für den Mittelwert.

\[\begin{split} \begin{array}{l} \hline \ \text{Schritt 1} & \text{Geben Sie die Nullhypothese } H_0 \text{ und alternative Hypothese } H_A \text{ an.}\\ \ \text{Schritt 2} & \text{Legen Sie das Signifikanzniveau, } \alpha\text{ fest.} \\ \ \text{Schritt 3} & \text{Berechnen Sie den Wert der Teststatistik.} \\ \ \text{Schritt 4} &\text{Bestimmen Sie den p-Wert.} \\ \ \text{Schritt 5} & \text{Wenn }p \le \alpha \text{, } H_0 \text{ ablehnen } \text{; ansonsten } H_0 \text{ nicht ablehnen} \text{.} \\ \ \text{Schritt 6} &\text{Interpretieren Sie das Ergebnis des Hypothesentests.} \\ \hline \end{array} \end{split}\]

Die Teststatistik für einen Hypothesentest mit der Nullhypothese \(H_0: \,\sigma = \sigma_0\) für eine normalverteilte Variable ist gegeben durch

\[\chi^2 = \frac{n-1}{\sigma^2_0}s^2\]

wobei \(n\) der Stichprobenumfang und \(s\) die Standardabweichung der Stichprobendaten ist.

Die Variable folgt einer \(\chi^2\)-Verteilung mit \(n-1\) Freiheitsgraden.

Beachten Sie, dass der Test auf eine Standardabweichung \(\chi^2\)-Test nicht robust gegenüber Abweichungen von der Normalverteilung ist (Weiss 2010).

\(\chi^2\) -Test auf Standardabweichung : Ein Beispiel

Um praktische Erfahrungen zu sammeln, wenden wir den \(\chi^2\)-Test mit einer Standardabweichung in einer Übung an. Dazu laden wir den students Datensatz. Sie können die Datei students.csv hier herunterladen. Importieren Sie den Datensatz und geben Sie ihm einen passenden Namen.

# Lese Datei students.csv als Dataframe ein; Indexspalte wird übersprungen
students = pd.read_csv("../../data/students.csv", index_col=0)

Der students Datensatz besteht aus \(8239\) Zeilen, von denen jede einen bestimmten Studenten repräsentiert, und \(16\) Spalten, von denen jede einer Variable/einem Merkmal entspricht, das sich auf diesen bestimmten Studenten bezieht. Diese selbsterklärenden Variablen sind: stud_id, name, gender, age, height, weight, religion, nc_score, semester, major, minor, score1, score2, online_tutorial, graduated, salary.

Um den \(\chi^2\)-Test auf Standardabweichung zu demonstrieren, untersuchen wir die Streuung der Körpergröße in cm der Studentinnen und vergleichen sie mit der Streuung der Körpergröße aller Studenten (unserer Grundgesamtheit). Wir wollen testen, ob die Standardabweichung der Körpergröße der Studentinnen kleiner ist als die Standardabweichung der Körpergröße aller Studenten.

Vorbereitung der Daten

Wir beginnen mit der Datenaufbereitung.

  • Zunächst definieren wir die Standardabweichung der Grundgesamtheit. In unserem Beispiel entspricht die Grundgesamtheit der Körpergröße aller \(8239\) Studenten im Datensatz. Wir berechnen die Standardabweichung für die Variable height und weisen ihr den Variablennamen sigma0 zu.

  • Zweitens unterteilen wir den Datensatz anhand der Variable gender.

  • Drittens nehmen wir eine Stichprobe von \(30\) Studentinnen und extrahieren die interessierende Statistik, die Standardabweichung der Größe der Studentinnen in unserer Stichprobe.

sigma0 = students["height"].std()
sigma0

11.077529134763823

Die Standardabweichung der interessierenden Grundgesamtheit (\(\sigma_0\)) beträgt \(\approx\) \(11,08\) cm.

female = students.loc[students["gender"] == "Female"]

n = 30
female_sample = female["height"].sample(n=30, random_state=1)
sample_std = female_sample.std()

Außerdem überprüfen wir die Normalverteilungsannahme, indem wir ein Q-Q-Diagramm erstellen. In Python können wir die Funktion qqplot() verwenden, um Q-Q-Plots zu erstellen.

# Erzeuge Q-Q Plot
qqp = smi.qqplot(female_sample, line="r")
ax = qqp.gca()
ax.set_title(
    "Q-Q-Diagramm für die Körpergrösse der \n in der Stichprobe befindlichen Studentinnen"
)
ax.set_xlabel("Theoretische Quantillen")
ax.set_ylabel("Stichproben Quantillen")

Text(0, 0.5, 'Stichproben Quantillen')
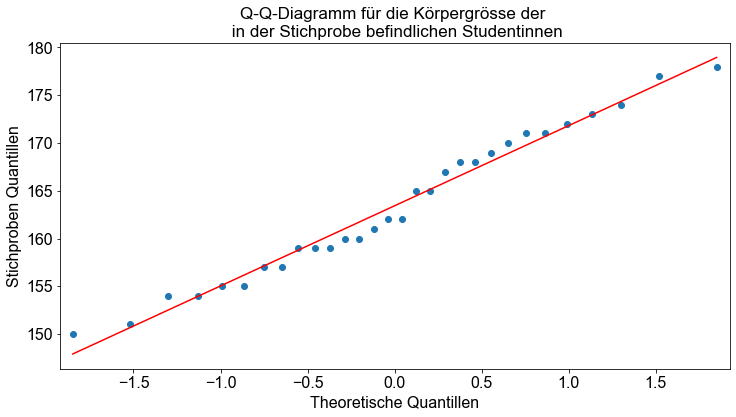
../_images/04_Standardabweichung_der_Grundgesamtheit_30_1.png

Wir sehen, dass die Daten ungefähr auf einer Geraden liegen. Auf der Grundlage des grafischen Auswertungsansatzes kommen wir zu dem Schluss, dass die interessierende Variable ungefähr normalverteilt ist.

Überprüfung der Hypothesen

Zur Durchführung des \(\chi^2\)-Tests auf Standardabweichung folgen wir dem Verfahren der schrittweisen Durchführung von Hypothesentests.

Schritt 1 : Geben Sie die Nullhypothese \(H_0\) und alternative Hypothese \(H_A\) an

Die Nullhypothese besagt, dass die Standardabweichung der Körpergröße der Studentinnen (\(\sigma\)) gleich der Standardabweichung der Grundgesamtheit (\(\sigma_0 \approx 11,08\) cm) ist.

\[H_0: \quad \sigma = \sigma_0\]

Alternative Hypothese

\[H_A: \quad \sigma < \sigma_0\]

Diese Formulierung führt zu einem linksseitigen Hypothesentest.

Schritt 2: Legen Sie das Signifikanzniveau,\(\alpha\) fest

\[\alpha = 0,05\]
alpha = 0.05

Schritt 3 und 4: Berechnen Sie den Wert der Teststatistik und den \(p\)-Wert

Zur Veranschaulichung berechnen wir die Teststatistik manuell in Python. Erinnern Sie sich an die Gleichung für die Teststatistik von oben:

\[\chi^2 = \frac{n-1}{\sigma^2_0}s^2\]
# Berechne Teststatistik
n = len(female_sample)
s_2 = np.var(female_sample,ddof=1)
sigma0_2 = np.var(students["height"],ddof=1)
x2 = ((n - 1) / sigma0_2) * s_2
x2

14.272211660048107

Der numerische Wert der Teststatistik ist \(14,27221166\).

Um den \(p\)-Wert zu berechnen, wenden wir die Funktion chi2.ppf() an. Erinnern Sie sich daran, wie man die Freiheitsgrade berechnet:

\[df=n-1\]
# Berechne df
df = n - 1

# Berechne p-Wert
p = chi2.cdf(x2, df=df)
p

0.010089951471801363

Schritt 5: Wenn \(p \le \alpha , H_0\) ablehnen; ansonsten \(H_0\) nicht ablehnen

p <= alpha

True

Der \(p\)-Wert ist kleiner als das angegebene Signifikanzniveau von \(0,05\); wir verwerfen \(H_0\). Die Testergebnisse sind statistisch signifikant auf dem \(5 \%\)-Niveau und liefern starke Beweise gegen die Nullhypothese.

Schritt 6: Interpretieren Sie das Ergebnis des Hypothesentests

\(p=0,01008995\). Bei einem Signifikanzniveau von \(5 \%\) lassen die Daten den Schluss zu, dass die Standardabweichung der Körpergröße von Studentinnen weniger als \(11\) cm beträgt.

Hypothesentests in Python

Wir haben gerade einen \(\chi^2\)-Test mit einer Standardabweichung in Python manuell durchgeführt. Meines Wissens bietet Python keine eingebaute Funktion zur Berechnung eines Standardabweichung \(\chi^2\)-Test. Wir können jedoch eine solche Funktion selbst implementieren. Unsere Funktion simple_chi2_test() nimmt als Eingabe einen Stichprobenvektor x, die Standardabweichung der Grundgesamtheit sigma0, das Signifikanzniveau alpha und die angegebene Methode, right, left und two-sided.

def simple_chi2_test(x, sigma0, alpha, method="two-sided"):
    df = len(x) - 1
    v = np.var(x,ddof=1)
    # Berechne Teststatistik
    testchi = df / (sigma0**2) * v

    # linksseitiger Test
    if method == "left":
        p = chi2.cdf(x=testchi, df=df)
    # rechtsseitiger Test
    elif method == "right":
        p = 1 - chi2.cdf(x=testchi, df=df)

    # beidseitiger Test (default)
    else:
        p_upper = 1 - chi2.cdf(x=testchi, df=df)
        p_lower = chi2.cdf(x=testchi, df=df)
        if p_upper * 2 > 1:
            p = p_lower * 2
        else:
            p = p_upper * 2
    # evaluiere p < alpha
    if p < alpha:
        reject = True
    else:
        reject = False

    # Ausgabe
    print("Significance level:", alpha)
    print("Degrees of freedom:", df)
    print("Test statistic:", round(testchi, 4))
    print("p-value:", p)
    print("Reject H0:", reject)

Wenden wir nun unsere selbst erstellte Funktion simple_x2_test() auf die obigen Beispieldaten an.

simple_chi2_test(x=female_sample, sigma0=sigma0, alpha=0.05, method="left")

Significance level: 0.05
Degrees of freedom: 29
Test statistic: 14.2722
p-value: 0.010089951471801363
Reject H0: True

Perfekt! Vergleichen Sie die Ausgabe der Funktion simple_chi2_test() mit unserem Ergebnis von oben. Auch hier können wir zu dem Schluss kommen, dass die Daten bei einem Signifikanzniveau von \(5 \%\) starke Anhaltspunkte dafür liefern, dass die Standardabweichung der Körpergröße von Studentinnen weniger als \(11\) cm beträgt.

%matplotlib inline
# Load the "autoreload" extension
%load_ext autoreload
# always reload modules
%autoreload 2
# black formatter for jupyter notebooks
#%load_ext nb_black
# black formatter for jupyter lab
%load_ext lab_black

%run ../../src/notebook_env.py

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload
The lab_black extension is already loaded. To reload it, use:
  %reload_ext lab_black

---------------------------------
Working on the host: Joachims-MacBook-Pro.local

---------------------------------
Python version: 3.10.2 | packaged by conda-forge | (main, Feb  1 2022, 19:30:18) [Clang 11.1.0 ]

---------------------------------
Python interpreter: /opt/miniconda3/envs/srh/bin/python

<Figure size 864x432 with 0 Axes>

Inferenz für Standardabweichungen zweier Grundgesamtheiten

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from random import sample
from scipy.stats import f
import statsmodels.api as smi

In diesem Abschnitt werden Hypothesentests für die Standardabweichungen zweier Grundgesamtheiten behandelt. Oder anders ausgedrückt, wir erörtern Methoden der Inferenz für die Standardabweichungen einer Variablen aus zwei verschiedenen Grundgesamtheiten. Diese Methoden beruhen auf der \(F\)-Verteilung, benannt zu Ehren von Sir Ronald Aylmer Fisher.

Die \(F\)-Verteilung ist eine rechtsschiefe Wahrscheinlichkeitsdichteverteilung mit zwei Formparametern, \(v_1\) und \(v_2\), den Freiheitsgraden für den Zähler (\(v_1\)) und den Freiheitsgraden für den Nenner (\(v_2\)).

\[df = (v_1,v_2)\]

Wie bei jeder anderen Dichtekurve entspricht die Fläche unter der Kurve der \(F\)-Verteilung den Wahrscheinlichkeiten. Die Fläche unter der Kurve und damit die Wahrscheinlichkeit für ein gegebenes Intervall und einen gegebenen \(df\)-Wert wird mittels Software berechnet. Alternativ kann man sie auch in einer Tabelle nachschlagen. In diesen Tabellen werden im Allgemeinen die Freiheitsgrade für den Zähler (\(v_1\)) am oberen Rand angezeigt, während die Freiheitsgrade für den Nenner (\(v_2\)) in den äußeren Spalten auf der linken Seite angezeigt werden.

Um einen Hypothesentest für zwei Grundgesamtheitsstandardabweichungen durchzuführen, wird der Wert berechnet, der einer bestimmten Fläche unter einer \(F\)-Kurve entspricht, berechnet.

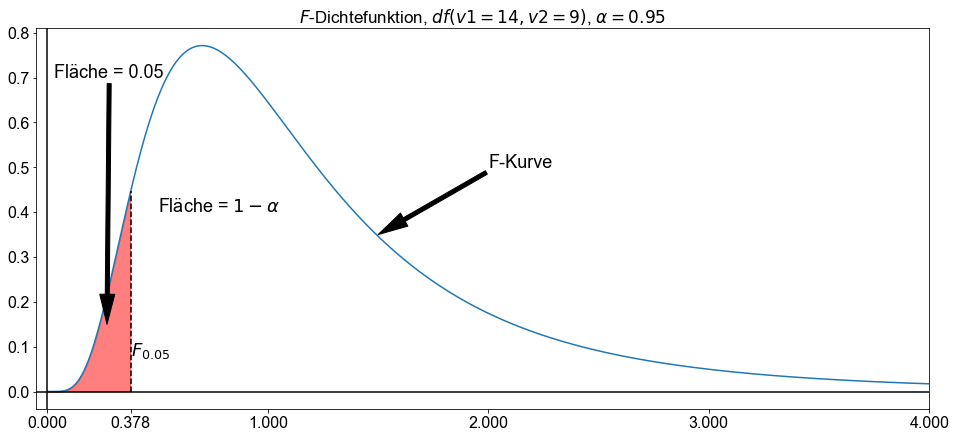
Für gegebenes \(\alpha\),wobei \(\alpha\) einer Wahrscheinlichkeit zwischen \(0\) und \(1\) entspricht, bezeichnet \(F_\alpha\) den Wert, der eine Fläche \(\alpha\) zu seiner Rechten unter einer \(F\)-Kurve hat.

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

v1 = 9
v2 = 14
alpha = 0.95
x = np.linspace(0, 5, 1000)
fig, ax = plt.subplots(figsize=(16, 7))
ax.plot(x, f.pdf(x, v1, v2))
ax.set_xlim(-0.05, 4)
ax.axvline(0, color="k")
ax.axhline(0, color="k")
ax.vlines(
    f.ppf(alpha, v1, v2),
    ymin=0,
    ymax=f.pdf(f.ppf(alpha, v1, v2), v1, v2),
    color="k",
    linestyle="dashed",
)

ax.fill_between(
    x, f.pdf(x, v1, v2), where=x >= f.ppf(alpha, v1, v2), color="r", alpha=0.5
)

ax.set_title(r"$F$-Dichtefunktion, $df(v1=9, v2=14)$, $\alpha=0.05$")


ax.annotate(
    r"F-Kurve",
    xy=(1.5, 0.35),
    xytext=(2, 0.5),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=18,
)

ax.annotate(
    r"Fläche = 0.05",
    xy=(2.9, 0.015),
    xytext=(3, 0.3),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=18,
)

ax.text(s="$F_{0.05}$", x=f.ppf(alpha, v1, v2), y=0.08, size=18)
ax.text(s=r"Fläche = $1 - \alpha$", x=0.5, y=0.4, size=18)

ticks = [0, 1, 2, f.ppf(alpha, v1, v2), 3, 4]
ax.set_xticks(ticks)

[<matplotlib.axis.XTick at 0x16dbebe20>,
 <matplotlib.axis.XTick at 0x16dbeaf20>,
 <matplotlib.axis.XTick at 0x16da47880>,
 <matplotlib.axis.XTick at 0x16dc20a60>,
 <matplotlib.axis.XTick at 0x16dc21f60>,
 <matplotlib.axis.XTick at 0x16dc22590>]
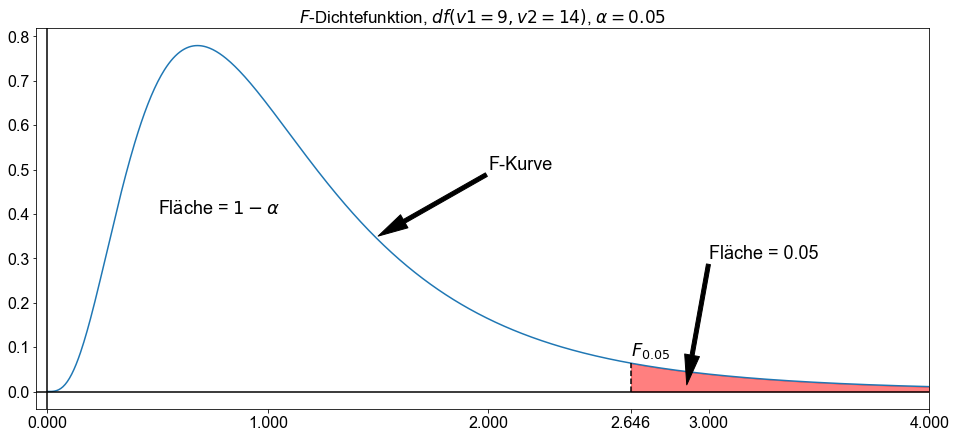
../_images/04_Standardabweichung_der_Grundgesamtheit_67_1.png

In der obigen Abbildung ergibt \(F_{0,05}\) für \(df=(9,14)\) den Wert \(\approx 2,6458\).

Eine interessante Eigenschaft von \(F\)-Kurven ist die reziproke Charakteristik. Sie besagt, dass für eine \(F\)-Kurve mit \(df=(v_1,v_2)\) der \(F\)-Wert mit der Fläche \(\alpha\) auf der linken Seite gleich dem Kehrwert des \(F\)-Wertes mit der Fläche \(\alpha\) auf der rechten Seite für eine \(F\)-Kurve mit \(df=(v_2,v_1)\) ist (Fahrmeir et al. [2016] s.282). Übertragen auf das obige Beispiel, bei dem \(F_{0,05}\) für \(df=(9,14) \approx 2,6458\) beträgt, bedeutet dies, dass \(F_{0,95}\) für \(df=(14,9) \ ; \ \frac{1}{2,6458}=0,378\) beträgt.

from scipy.stats import chi2
import numpy as np
import matplotlib.pyplot as plt

v1 = 14
v2 = 9
alpha = 0.05
x = np.linspace(0, 5, 1000)
fig, ax = plt.subplots(figsize=(16, 7))
ax.plot(x, f.pdf(x, v1, v2))
ax.set_xlim(-0.05, 4)
ax.axvline(0, color="k")
ax.axhline(0, color="k")
ax.vlines(
    f.ppf(alpha, v1, v2),
    ymin=0,
    ymax=f.pdf(f.ppf(alpha, v1, v2), v1, v2),
    color="k",
    linestyle="dashed",
)

ax.fill_between(
    x, f.pdf(x, v1, v2), where=x <= f.ppf(alpha, v1, v2), color="r", alpha=0.5
)

ax.set_title(r"$F$-Dichtefunktion, $df(v1=14, v2=9)$, $\alpha=0.95$")


ax.annotate(
    r"F-Kurve",
    xy=(1.5, 0.35),
    xytext=(2, 0.5),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=18,
)

ax.annotate(
    r"Fläche = 0.05",
    xy=(0.27, 0.15),
    xytext=(0.28, 0.7),
    # textcoords="data",
    arrowprops=dict(headwidth=15, headlength=30, width=4, color="k"),
    size=18,
    horizontalalignment="center",
)

ax.text(s="$F_{0.05}$", x=f.ppf(alpha, v1, v2), y=0.08, size=18)
ax.text(s=r"Fläche = $1 - \alpha$", x=0.5, y=0.4, size=18)

ticks = [0, 1, 2, f.ppf(alpha, v1, v2), 3, 4]
ax.set_xticks(ticks)

[<matplotlib.axis.XTick at 0x16dceb730>,
 <matplotlib.axis.XTick at 0x16dceb760>,
 <matplotlib.axis.XTick at 0x16dceb880>,
 <matplotlib.axis.XTick at 0x16dd4ce80>,
 <matplotlib.axis.XTick at 0x16dd4d5d0>,
 <matplotlib.axis.XTick at 0x16dd4dd20>]
../_images/04_Standardabweichung_der_Grundgesamtheit_69_1.png

Intervall-Schätzung von \(\sigma_1-\sigma_2\)

Das \(100(1-\alpha)\%\)-Konfidenzintervall für \(\sigma\) beträgt

\[\frac{1}{\sqrt{F_{\alpha /2}}} \times \frac{s_1}{s_2} \le \sigma \le \frac{1}{\sqrt{F_{1-\alpha /2}}} \times \frac{s_1}{s_2}\text{,}\]

wobei \(s_1\) und \(s_2\) die Standardabweichungen der Stichprobe sind.

\(F\)-Test für zwei Standardabweichungen

Das Hypothesentestverfahren für die Standardabweichung wird als F-Test für zwei Standardabweichungen bezeichnet. Der Hypothesentest für zwei Standardabweichungen der Grundgesamtheit folgt demselben schrittweisen Verfahren wie andere Hypothesentests.

\[\begin{split} \begin{array}{l} \hline \ \text{Schritt 1} & \text{Geben Sie die Nullhypothese } H_0 \text{ und alternative Hypothese } H_A \text{ an.}\\ \ \text{Schritt 2} & \text{Legen Sie das Signifikanzniveau, } \alpha\text{ fest.} \\ \ \text{Schritt 3} & \text{Berechnen Sie den Wert der Teststatistik.} \\ \ \text{Schritt 4} &\text{Bestimmen Sie den p-Wert.} \\ \ \text{Schritt 5} & \text{Wenn }p \le \alpha \text{, } H_0 \text{ ablehnen } \text{; ansonsten } H_0 \text{ nicht ablehnen} \text{.} \\ \ \text{Schritt 6} &\text{Interpretieren Sie das Ergebnis des Hypothesentests.} \\ \hline \end{array} \end{split}\]

Die Teststatistik für einen Hypothesentest für eine normalverteilte Variable und für unabhängige Stichproben der Größen \(n_1\) und \(n_2\) ist gegeben durch

\[F = \frac{s_1^2/\sigma_1^2}{s_2^2/\sigma_2^2}\text{,}\]

mit \(df=(n_1-1,n_2-1)\).

Wenn \(H_0: \sigma_1 = \sigma_2\) wahr ist, dann vereinfacht sich die Gleichung zu

\[F = \frac{s_1^2}{s_2^2}\]

\(F\)-Test für zwei Standardabweichungen : Ein Beispiel

Um einige praktische Erfahrungen zu sammeln, wenden wir den \(F\)-Test für zwei Standardabweichungen in einer Übung an. Dazu laden wir den students Datensatz. Sie können die Datei students.csv hier herunterladen. Importieren Sie den Datensatz und geben Sie ihm einen passenden Namen.

# Lese Datei students.csv als Dataframe ein; Indexspalte wird übersprungen
students = pd.read_csv("../../data/students.csv", index_col=0)

Der students Datensatz besteht aus \(8239\) Zeilen, von denen jede einen bestimmten Studenten repräsentiert, und \(16\) Spalten, von denen jede einer Variable/einem Merkmal entspricht, das sich auf diesen bestimmten Studenten bezieht. Diese selbsterklärenden Variablen sind: stud_id, name, gender, age, height, weight, religion, nc_score, semester, major, minor, score1, score2, online_tutorial, graduated, salary.

Um den \(F\)-Test für zwei Standardabweichungen zu zeigen, untersuchen wir die Streuung der Körpergröße in cm der Studentinnen und vergleichen sie mit der Streuung der Körpergröße aller Studenten (unserer Grundgesamtheit). Wir wollen testen, ob sich die Standardabweichung der Körpergröße der weiblichen Studenten (\(\sigma_1\)) von der Standardabweichung der Körpergröße der männlichen Studenten (\(\sigma_2\)) unterscheidet.

Vorbereitung der Daten

  • Wir unterteilen den Datensatz anhand der Variable gender.

  • Dann nehmen wir \(25\) weibliche und \(25\) männliche Studenten in die Stichprobe auf.

  • Dann berechnen wir die Standardabweichungen der interessierenden Variable (Körpergröße in cm) für beide Stichproben und weisen ihnen die Variablen std_female und std_male zu.

# Unterteile Datensatz nach Variable `gender`
male = students.loc[students["gender"] == "Male"]
female = students.loc[students["gender"] == "Female"]

# Entnehme Probe von jeweils 25 Studenten
n = 25
male_sample = male["height"].sample(n=25, random_state=1)
female_sample = female["height"].sample(n=25, random_state=1)

std_female = np.std(female_sample, ddof=1)
std_female

7.009041779492163

std_male = np.std(male_sample, ddof=1)
std_male

8.203251387915241

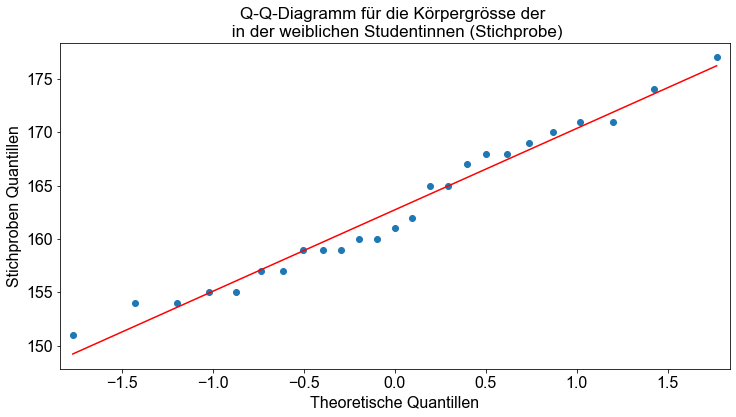
Außerdem überprüfen wir die Normalverteilungsannahme, indem wir ein Q-Q-Diagramm erstellen. In Python können wir die Funktion qqplot() verwenden, um Q-Q-Plots zu erstellen.

# Erzeuge Q-Q Plot
qqp = smi.qqplot(female_sample, line="r")
ax = qqp.gca()
ax.set_title(
    "Q-Q-Diagramm für die Körpergrösse der \n in der weiblichen Studentinnen (Stichprobe)"
)
ax.set_xlabel("Theoretische Quantillen")
ax.set_ylabel("Stichproben Quantillen")

Text(0, 0.5, 'Stichproben Quantillen')
../_images/04_Standardabweichung_der_Grundgesamtheit_92_1.png 
# Erzeuge Q-Q Plot
qqp = smi.qqplot(male_sample, line="r")
ax = qqp.gca()
ax.set_title(
    "Q-Q-Diagramm für die Körpergrösse der \n in der männlichen Studenten (Stichprobe)"
)
ax.set_xlabel("Theoretische Quantillen")
ax.set_ylabel("Stichproben Quantillen")

Text(0, 0.5, 'Stichproben Quantillen')
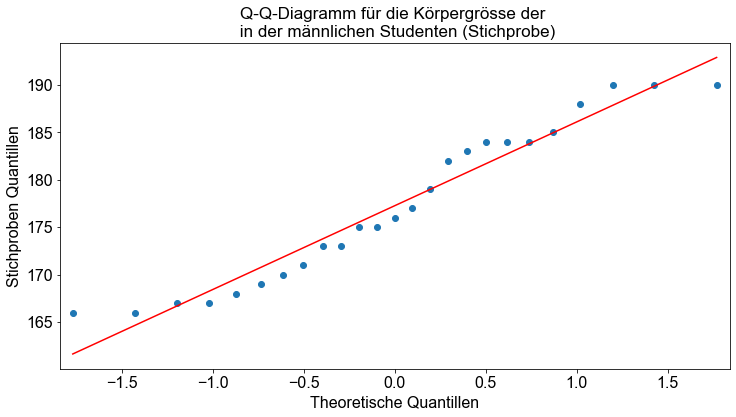
../_images/04_Standardabweichung_der_Grundgesamtheit_93_1.png

Wir sehen, dass die Daten ungefähr auf einer Geraden liegen. Auf der Grundlage des grafischen Auswertungsansatzes kommen wir zu dem Schluss, dass die interessierende Variable ungefähr normalverteilt ist.

Überprüfung der Hypothesen

Zur Durchführung des \(F\)-Tests für zwei Standardabweichungen folgen wir dem Verfahren der schrittweisen Durchführung von Hypothesentests.

Schritt 1 : Geben Sie die Nullhypothese \(H_0\) und alternative Hypothese \(H_A\) an

Die Nullhypothese besagt, dass die Standardabweichung der Körpergröße der weiblichen Studenten (\(\sigma_1\)) gleich der Standardabweichung der Körpergröße der männlichen Studenten (\(\sigma_2\)) ist.

\[H_0: \quad \sigma_1 = \sigma_2\]

Alternative Hypothese

\[H_A: \quad \sigma_1 \ne \sigma_2\]

Diese Formulierung führt zu einem zweiseitigen Hypothesentest.

Schritt 2: Legen Sie das Signifikanzniveau,\(\alpha\) fest

\[\alpha = 0,05\]
alpha = 0.05

Schritt 3 und 4: Berechnen Sie den Wert der Teststatistik und den \(p\)-Wert

Zur Veranschaulichung berechnen wir die Teststatistik manuell in Python. Erinnern Sie sich an die Gleichung für die Teststatistik von oben:

\[F = \frac{s_1^2}{s_2^2}\]
# Berechne die Teststatistik
Ftest = std_female**2 / std_male**2
Ftest

0.7300376461264116

Der numerische Wert der Teststatistik beträgt \(\approx 0,73\).

Um den \(p\)-Wert zu berechnen, wenden wir die Funktion f.cdf() an. Erinnern Sie sich daran, wie man die Freiheitsgrade berechnet.

\[df = (n_1 - 1, n_2 - 1)\]
# Berechne df
df1 = len(female_sample) - 1
df2 = len(male_sample) - 1

# Berechne p-Wert
p_upper = 1 - f.cdf(Ftest, dfn=df1, dfd=df2)
p_lower = f.cdf(Ftest, dfn=df1, dfd=df2)

if p_upper * 2 > 1:
    p = p_lower * 2
else:
    p = p_upper * 2
p

0.4465246946119613

Schritt 5: Wenn \(p \le \alpha , H_0\) ablehnen; ansonsten \(H_0\) nicht ablehnen

p <= alpha

False

Der \(p\)-Wert ist größer als das angegebene Signifikanzniveau von \(0,05\); wir verwerfen \(H_0\) nicht. Die Testergebnisse sind auf dem \(5 \%\)-Niveau statistisch signifikant und liefern keinen ausreichenden Beweis gegen die Nullhypothese.

Schritt 6: Interpretieren Sie das Ergebnis des Hypothesentests

\(p=0,44652469\). Bei einem Signifikanzniveau von \(5 \%\) liefern die Daten keine ausreichenden Beweise für die Schlussfolgerung, dass die Standardabweichungen der Körpergröße von weiblichen und männlichen Studenten unterschiedlich sind.

Hypothesentests in Python

Wir haben gerade einen \(F\)-Test für zwei Standardabweichungen in Python manuell durchgeführt. OK, wir haben eine Menge gelernt, aber jetzt nutzen wir die Mittel von Python, um das gleiche Ergebnis wie oben mit nur einer Zeile Code zu erhalten!

Um einen \(F\)-Test für zwei Standardabweichungen in Python durchzuführen, verwenden wir unsere Funktion simple_x2_test() und verändern sie geringfügig. Wir geben zwei Vektoren als Dateneingabe an: female_sample und male_sample. Das Argument alternative muss nicht angegeben werden, da alternative = 'two-sided' die Vorgabe ist.

def simple_f_test(x, y, dfn, dfd, alpha, method="two-sided"):
    df1 = len(female_sample) - 1
    df2 = len(male_sample) - 1
    std_male = np.std(male_sample, ddof=1)
    std_female = np.std(female_sample, ddof=1)
    # Berechne Teststatistik
    Ftest = std_female**2 / std_male**2

    # linksseitiger Test
    if method == "left":
        p = scipy.stats.f.cdf(x=Ftest, dfn=df1, dfd=df2)
    # rechtsseitiger Test
    elif method == "right":
        p = 1 - scipy.stats.f.cdf(x=Ftest, dfn=df1, dfd=df2)

    # beidseitiger Test (default)
    else:
        p_upper = 1 - f.cdf(Ftest, dfn=df1, dfd=df2)
        p_lower = f.cdf(Ftest, dfn=df1, dfd=df2)

    if p_upper * 2 > 1:
        p = p_lower * 2
    else:
        p = p_upper * 2
    # evaluiere p < alpha
    if p < alpha:
        reject = True
    else:
        reject = False

    # Ausgabe
    print("Significance level:", alpha)
    print("Degrees of freedom:", df1, df2)
    print("Test statistic:", round(Ftest, 4))
    print("p-value:", p)
    print("Reject H0:", reject)

simple_f_test(female_sample, male_sample, df1, df2, alpha=alpha)

Significance level: 0.05
Degrees of freedom: 24 24
Test statistic: 0.73
p-value: 0.4465246946119613
Reject H0: False

Es hat gut funktioniert! Vergleichen Sie die Ausgabe der Funktion simple_f_test() mit unserem Ergebnis von oben. Auch hier können wir zu dem Schluss kommen, dass die Daten bei einem Signifikanzniveau von \(5 \%\) keine ausreichenden Beweise dafür liefern, dass die Standardabweichungen der Körpergröße von weiblichen und männlichen Studenten unterschiedlich sind.

previous

Hypothesentests für zwei Grundgesamtheitsmittelwerte

next

Chi-Quadrat-Tests