Die Student t-Verteilung
Contents
Die Student t-Verteilung¶
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import t
Die Studentsche \(t\)-Verteilung ist nach William Sealy Gosset (\(1876-1937\)) benannt, der sie \(1908\) erstmals bestimmte. Gosset war einer der besten Oxford-Absolventen in Chemie und Mathematik seiner Generation. Im Jahr \(1899\) nahm er eine Stelle als Brauer bei Arthur Guinness Son & Co, Ltd in Dublin, Irland, an. Bei seiner Arbeit für die Guinness-Brauerei interessierte er sich für die Qualitätskontrolle anhand kleiner Proben in verschiedenen Stadien des Produktionsprozesses. Da Guinness seinen Angestellten die Veröffentlichung von Papieren untersagte, um die Weitergabe vertraulicher Informationen zu verhindern, hatte Gosset seine Arbeit unter dem Pseudonym “Student” veröffentlicht, und seine Identität war einige Zeit nach der Veröffentlichung seiner berühmtesten Errungenschaften nicht bekannt, so dass die Verteilung den Namen “Studentsche” oder “\(t\)-Distribution” erhielt, wodurch sein Name weniger bekannt wurde als seine wichtigen Ergebnisse in der Statistik ([Dümbgen, 2016] s.81).
Die \(t\)-Verteilungskurve ist, wie die Normalverteilungskurve, symmetrisch (glockenförmig) um den Mittelwert. Die \(t\)-Verteilungskurve ist jedoch flacher als die Standard-Normalverteilungskurve. Folglich hat die \(t\)-Verteilungskurve eine geringere Höhe und eine breitere Streuung als die Standardnormalverteilung.
Die \(t\)-Verteilung hat nur einen Parameter, die sogenannten Freiheitsgrade (\(df\)). Die Form einer bestimmten \(t\)-Verteilungskurve hängt von der Anzahl der Freiheitsgrade (\(df\)) ab. Die Anzahl der Freiheitsgrade für eine \(t\)-Verteilung ist gleich dem Stichprobenumfang minus eins, das heißt,
Wenn der Stichprobenumfang \(n\) und damit \(df\) zunimmt, nähert sich die \(t\)-Verteilung der Standardnormalverteilung an. Die Einheiten einer \(t\)-Verteilung werden mit \(t\) bezeichnet. Der Mittelwert der \(t\)-Verteilung ist gleich \(0\), und ihre Standardabweichung beträgt \( \sqrt{df/(df-2)}\) ([Fahrmeir et al., 2016] s.280,s.284).
import numpy as np
from scipy.stats import t, norm
import matplotlib.pyplot as plt
df = [1, 3, 8, 30]
x = np.linspace(-4, 4, 1000)
fig, ax = plt.subplots()
for _df in df:
ax.plot(x, t.pdf(x, df=_df), label=f"df={_df}")
ax.plot(x, norm.pdf(x), label=f"normal", color="k", linestyle="dashed")
ax.vlines(x=0, ymin=0, ymax=norm.pdf(0, 0, 1), color="k")
ax.set_yticks([])
ax.set_title(
"Vergleich der t-Warscheinlichkeitsdichtefunktion\nmit unterschiedlichen Freiheitsgraden (df) und\nder Warscheinlichkeitsdichtefunktion der Normalverteilung"
)
ax.legend(fontsize=18)
<matplotlib.legend.Legend at 0x111120760>
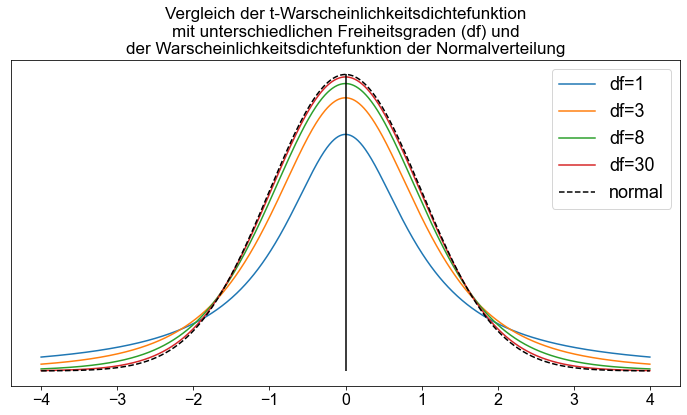
Grundlegende Eigenschaften von t-Kurven¶
Die Gesamtfläche unter einer \(t\)-Kurve ist gleich \(1\).
Eine \(t\)-Kurve erstreckt sich unendlich in beide Richtungen und nähert sich dabei der horizontalen Achse, berührt sie aber nie.
Eine \(t\)-Kurve ist symmetrisch um \(0\).
Mit zunehmender Anzahl von Freiheitsgraden ähneln \(t\)-Kurven immer mehr der Standard-Normalverteilung.
Die Studentsche-t-Verteilung in Python¶
Python ermöglicht den Zugriff auf die \(t\)-Verteilung mit den Funktionen t.pdf(), t.cdf(), t.ppf() und t.rvs(). Wenden Sie die Funktion dir() auf diese Funktionen an, um weitere Informationen zu erhalten.
Die Funktion t.rvs() erzeugt Zufallsabweichungen der \(t\)-Verteilung und wird alst.rvs(df, loc , scale, size) geschrieben. Wir können leicht eine Anzahl von \(n\) Zufallsstichproben erzeugen. Erinnern Sie sich daran, dass die Anzahl der Freiheitsgrade für eine \(t\)-Verteilung gleich dem Stichprobenumfang minus eins ist, d.h.,
# Generiere Zufallswerte der t Verteilung mit df = 29 und Stichprobengrösse = 30
n = 30
t.rvs(df=n - 1, size=n)
array([ 8.09401246e-01, 4.12596116e-01, -7.06056142e-01, 1.94949752e+00,
-9.35870547e-02, -3.00706926e-01, -5.61210750e-01, -7.38019451e-01,
2.11174080e-01, 9.59300054e-01, -9.84381087e-01, 8.44623730e-01,
-2.92368737e+00, -6.81804616e-01, -4.74730799e-01, 2.08643823e-02,
-7.56447591e-01, 1.63023254e+00, -8.43113872e-01, -8.92673212e-02,
-3.17866753e-01, -5.74165678e-01, 5.04143883e-01, -7.24047949e-01,
-1.26241424e+00, -7.72689162e-01, -3.17398793e-01, -2.17120090e+00,
3.62647992e-01, -1.36706562e-03])
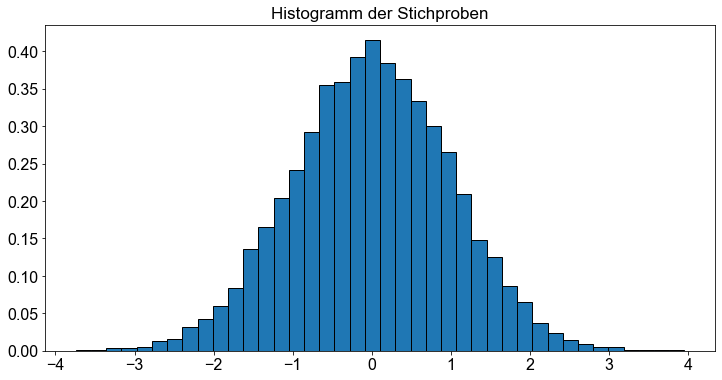
Außerdem können wir eine sehr große Anzahl von Stichproben erzeugen und sie als Histogramm darstellen.
# Generiere Zufallswerte der t Verteilung mit df = 9999 und Stichprobengrösse = 10000
n = 10000
y = t.rvs(df=n - 1, size=n)
fig, ax = plt.subplots()
ax.set_title("Histogramm der Stichproben")
_ = ax.hist(y, bins=40, density=True, edgecolor="k")
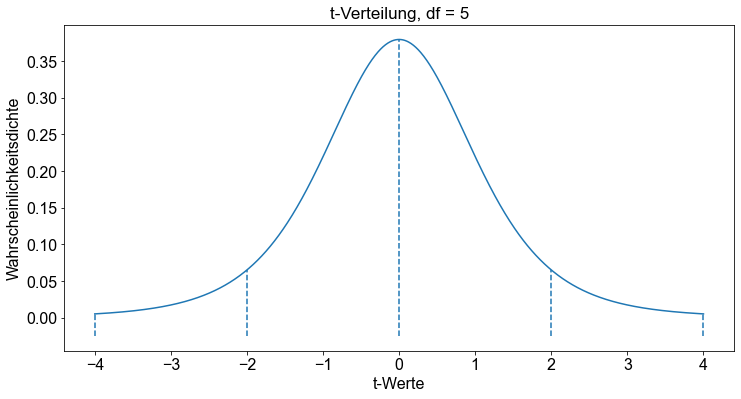
Mit der Funktion t.pdf() können wir die Wahrscheinlichkeitsdichtefunktion und damit den vertikalen Abstand zwischen der horizontalen Achse und der \(t\)-Kurve an jedem beliebigen Punkt berechnen. Zur Demonstration konstruieren wir eine \(t\)-Verteilung mit \(df=5\) und berechnen die Wahrscheinlichkeitsdichtefunktion bei \(t=-4,-2,0,2,4\).
x = [-4, -2, 0, 2, 4]
y_t = t.pdf(x, df=5)
y_t
array([0.00512373, 0.06509031, 0.37960669, 0.06509031, 0.00512373])
# Erzeuge x-werte
x = np.linspace(-4, 4, num=1000)
# Plotte t-Verteilung
fig, ax = plt.subplots()
ax.set_title("t-Verteilung, df = 5")
ax.set_xlabel("t-Werte")
ax.set_ylabel("Wahrscheinlichkeitsdichte")
ax.plot(x, t.pdf(x, df=5))
for _t in [-4, -2, 0, 2, 4]:
ax.vlines(_t, ymin=-0.025, ymax=t.pdf(_t, df=5), linestyle="dashed")
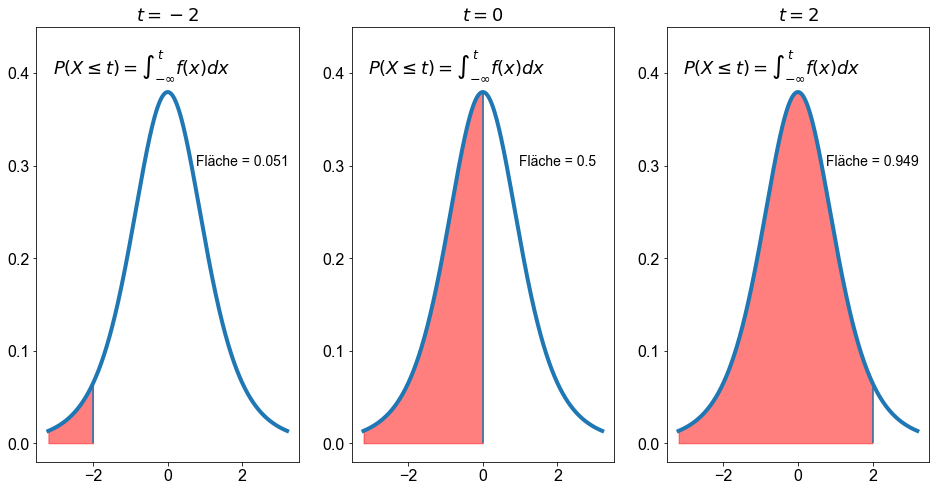
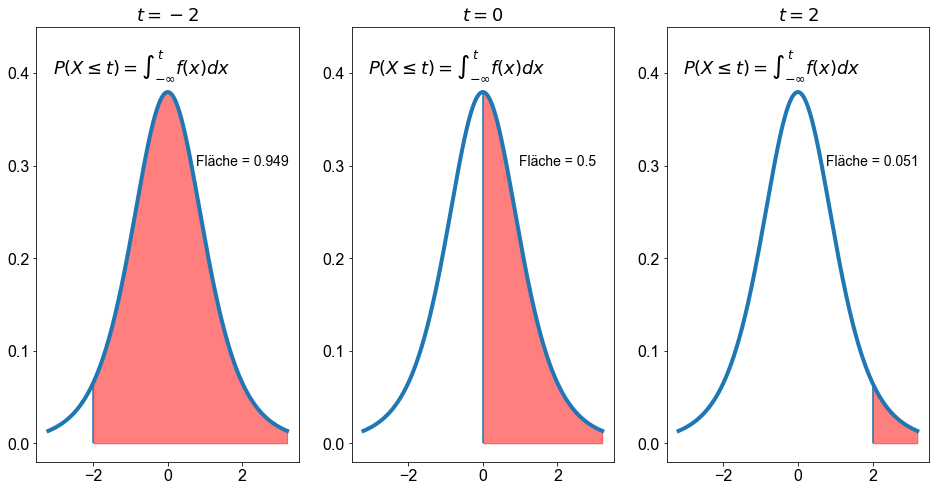
Eine weitere sehr nützliche Funktion ist die Funktion t.cdf(), die die Fläche unter der \(t\)-Kurve für ein beliebiges Intervall liefert. Berechnen wir die Fläche unter der Kurve für die Intervalle \(j_i= \ ]-\infty \ \),\( \ -2]\) , \(]-\infty \ \),\( \ 0]\) , \(]-\infty \ \),\( \ 2]\) und \(k_i=[-2 \ \),\( \ \infty[\) , \([0 \ \),\( \ \infty[\) , \([2 \ \),\( \ \infty[\) für eine Zufallsvariable mit einer \(t\)-Verteilung mit \(df=5\).
x_cdf_left = []
# Berechne kumulitative Wahrscheinlichkeit links von Wert _t
for _t in [-2, 0, 2]:
res = t.cdf(_t, df=5)
print(f"Wert für Fläche links von {_t}: {res}")
x_cdf_left.append(res)
Wert für Fläche links von -2: 0.05096973941492914
Wert für Fläche links von 0: 0.5
Wert für Fläche links von 2: 0.9490302605850709
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt
df = 5
fig, ax = plt.subplots(figsize=(16, 8), ncols=3)
# axis 0
x = np.linspace(-3.2, 3.2, 1000)
for e, _t in enumerate([-2, 0, 2]):
ax[e].plot(x, t.pdf(x, df=df), color="C0", linewidth=4)
ax[e].vlines(_t, ymin=0, ymax=t.pdf(_t, df=df))
ax[e].fill_between(x, t.pdf(x, df=df), where=x <= _t, color="r", alpha=0.5)
ax[e].text(
-0.7,
0.4,
s=r"$P(X \leq {t}) = \int_{-\infty}^{t}f(x)dx$",
horizontalalignment="center",
size=18,
)
ax[e].text(
2,
0.3,
s=f"Fläche = {np.round(t.cdf(_t, df=df),3)}",
horizontalalignment="center",
size=14,
)
ax[e].set_title(f"$t={_t}$", size=18)
for _ax in ax:
_ax.set_ylim(-0.02, 0.45)
x_cdf_right = []
# Berechne kumulitative Wahrscheinlichkeit rechts von Wert _t
for _t in [-2, 0, 2]:
res = 1 - t.cdf(_t, df=5)
print(f"Wert für Fläche rechts von {_t}: {res}")
x_cdf_right.append(res)
Wert für Fläche rechts von -2: 0.9490302605850709
Wert für Fläche rechts von 0: 0.5
Wert für Fläche rechts von 2: 0.050969739414929105
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt
df = 5
fig, ax = plt.subplots(figsize=(16, 8), ncols=3)
# axis 0
x = np.linspace(-3.2, 3.2, 1000)
for e, _t in enumerate([-2, 0, 2]):
ax[e].plot(x, t.pdf(x, df=df), color="C0", linewidth=4)
ax[e].vlines(_t, ymin=0, ymax=t.pdf(_t, df=df))
ax[e].fill_between(x, t.pdf(x, df=df), where=x >= _t, color="r", alpha=0.5)
ax[e].text(
-0.7,
0.4,
s=r"$P(X \leq {t}) = \int_{-\infty}^{t}f(x)dx$",
horizontalalignment="center",
size=18,
)
ax[e].text(
2,
0.3,
s=f"Fläche = {np.round(1-t.cdf(_t, df=df),3)}",
horizontalalignment="center",
size=14,
)
ax[e].set_title(f"$t={_t}$", size=18)
for _ax in ax:
_ax.set_ylim(-0.02, 0.45)
Die Funktion t.ppf() liefert die Quantilfunktion und ist damit die Umkehrfunktion von t.cdf(). Für die Intervalle \(j_i= ]-\infty \ \),\( \ -2]\) , \(]-\infty \ \),\( \ 0]\) , \(]-\infty \ \),\( \ 2]\) einer Zufallsvariablen, die einer \(t\)-Verteilung mit \(df=5\) folgt, liefert die Funktion t.ppf()…
x_cdf_left
[0.05096973941492914, 0.5, 0.9490302605850709]
for x in x_cdf_left:
print(f"{round(x,2)}: {round(t.ppf(x, df=5), 2)}")
0.05: -2.0
0.5: 0.0
0.95: 2.0
… und für die Intervalle \(k_i=[-2 \ \),\( \ \infty[\) , \([0 \ \),\( \ \infty[\) , \([2 \ \),\( \ \infty[\) einer Zufallsvariablen, die einer \(t\)-Verteilung mit \(df=5\) folgt, liefert die Funktion t.ppf
for x in x_cdf_right:
print(f"{round(x,2)}: {round(t.ppf(x, df=5), 2)}")
0.95: 2.0
0.5: 0.0
0.05: -2.0
